题目列表(包括答案和解析)
①函数f(x)=loga(1-x)在(-∞,0)上是减函数②(a-2)2(a-1)＞0 ③a(a-1)≥0 ④
＜1
A.①② B.③④ C.②③ D.②④
已知方程x2＋4ax＋3a＋1＝0(a>1)的两根为tanα、tanβ，且α，β∈
，则tan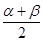
的值是( )
A.
B．－2 C.
D.或－2
函数y=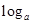
(|x|+1)(a>1)的图象大致是
函数y=a|x|(a>1)的图象是( )
曲线C是平面内与两个定点F1（-1，0）和F2（1，0）的距离的积等于常数 a2 (a >1)的点的轨迹.给出下列三个结论：
① 曲线C过坐标原点；
② 曲线C关于坐标原点对称；
③若点P在曲线C上，则△F
PF
的面积大于
a
。
其中，所有正确结论的序号是 。
一，选择题:
D C B CC， CA BC B
二、填空题：
(11),
-3
,
(12), 27
(13), 
(14), 
. (15), －26，14，65
三、解答题：
16, 由已知得
;所以解集:
;
17, （１）由题意
，
＝１又a＞０，所以a＝１．
（２）
g（x）＝
，当
时，
＝
，无递增区间；当x＜１时，＝
，它的递增区间是
．
综上知：的单调递增区间是．
18, （1）当0<t≤10时，
是增函数，且f(10)=240
当20<t≤40时，
是减函数，且f(20)=240 所以，讲课开始10分钟，学生的注意力最集中，能持续10分钟。（3）当0<t≤10时，令
，则t=4 当20<t≤40时，令
，则t≈28.57
则学生注意力在180以上所持续的时间28.57－4=24.57>24
从而教师可以第4分钟至第28.57分钟这个时间段内将题讲完。
19, （I）
……1分
根据题意，
…………4分
解得
. …………7分
（II）因为
……7分
（i）
时，函数
无最大值，
不合题意，舍去. …………11分
（ii）
时，根据题意得
解之得
…………13分
为正整数，=3或4. …………14分
20. （1）当x∈［－1,0）时, f(x)= f(－x)=loga［2－（－x）］=loga（2+x）.
当x∈［2k－1,2k），（k∈Z）时,x－2k∈［－1,0］, f(x)=f（x－2k）=loga［2+（x－2k）］.
当x∈［2k,2k+1］（k∈Z）时,x－2k∈［0,1］, f(x)=f（x－2k）=loga［2－（x－2k）］.
故当x∈［2k－1,2k+1］（k∈Z）时, f(x)的表达式为
|
=
,∴a=4.
得
得
－2＜x＜2k+2－
f(x)
恒成立，∴a=c=2 f(x)=2（x+1）2
=
，D={x?x
-1 }
，x2=
，x3=-
，x4=-1，∴M={