
题目列表(包括答案和解析)
如图![]() 、
、![]() 是单位圆
是单位圆![]() 上的点,
上的点,![]() 是圆与
是圆与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 点的坐标为
点的坐标为![]() ,三角形
,三角形![]() 为正三角形.
为正三角形.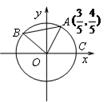
(Ⅰ)求![]() ;
;
(Ⅱ)求![]() 的值.
的值.
如图![]() 、
、![]() 是单位圆
是单位圆![]() 上的点,且
上的点,且![]() 在第二象限. 点
在第二象限. 点![]() 是圆
是圆![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() 的坐标为
的坐标为![]() ,若△
,若△![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() ;
;
(Ⅱ)求![]() .
.

(本小题满分10分)
如图: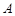 、
、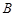 是单位圆
是单位圆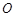 上的点,
上的点,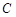 是圆与
是圆与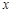 轴正半轴的交点,三角形
轴正半轴的交点,三角形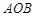 为正三角形, 且AB∥
为正三角形, 且AB∥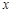 轴.
轴.
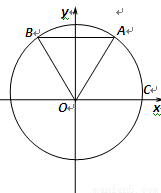
(1)求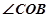 的三个三角函数值;
的三个三角函数值;
(2)求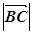 及
及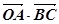 .
.
(本小题满分10分)
如图: 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥ 轴.
轴.
(1)求 的三个三角函数值;
的三个三角函数值;
(2)求 及
及 .
.
 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥ 轴.
轴.
 的三个三角函数值;
的三个三角函数值; 及
及 .
.1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B 
11.A 12.D
【解析】
1. ,所以选B.
,所以选B.
2. 的系数是
的系数是 ,所以选B.
,所以选B.
3. ,所以选
,所以选 .
.
4. 为钝角或
为钝角或 ,所以选C
,所以选C
5. ,所以选C.
,所以选C.
6. ,所以选B.
,所以选B.
7. ,所以选D.
,所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9.将 左移
左移 个单位得
个单位得 ,所以选A.
,所以选A.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.画可行域 可知符合条件的点 是:
是: 共6个点,故
共6个点,故 ,所以选D.
,所以选D.
二、
13.185. .
.
14.60. .
.
15. ,由
,由 ,得
,得
 .
.
16. .如图:
.如图:

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)由三角函数的定义知: .
.
(2)


 .
.
18.(1)设两年后出口额恰好达到危机前出口额的事件为 ,则
,则 .
.
(2)设两年后出口额超过危机前出口额的事件为 ,则
,则 .
.
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)


(2)

又


综上: .
.
21.(1) 的解集为(1,3)
的解集为(1,3)
∴1和3是 的两根且
的两根且
|