
题目列表(包括答案和解析)
| π | 2 |
(本题满分12分)已知单调递增的等比数列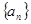 满足:
满足: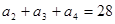 ,且
,且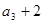 是
是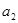 和
和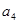 的等差中项.
的等差中项.
(1)求数列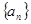 的通项公式
的通项公式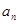 ;
;
(2)令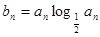 ,
,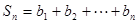 ,求使
,求使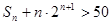 成立的小的正整数
成立的小的正整数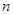 .
.
(本题满分12分)如图,已知直平行六面体ABCD—A![]() B
B![]() C
C![]() D
D![]() 中,AD⊥BD,AD=BD=a,E是CC
中,AD⊥BD,AD=BD=a,E是CC![]() 的中点,A1D⊥BE.
的中点,A1D⊥BE.
(1)求证:A![]() D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A
D⊥平面BDE;(2)求二面角B—DE—C的大小;(3)求点B到平面A![]() DE的距离.
DE的距离.
(本题满分12分)
已知动圆 过点
过点 ,且与圆
,且与圆 相内切.
相内切.
(1)求动圆 的圆心的轨迹方程;
的圆心的轨迹方程;
(2)设直线 (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D,与双曲线
,D,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
(本题满分12分)
如下图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB=20km,CB =10km ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为 km.
km.
(1)按下列要求写出函数关系式:
①设∠BAO=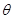 (rad),将
(rad),将 表示成
表示成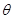 的函数;
的函数;
②设OP (km) ,将
(km) ,将 表示成
表示成 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com