
题目列表(包括答案和解析)
已知定义域为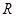 的函数
的函数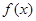 满足
满足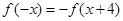 ,则
,则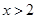 时,
时,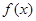 单调递增,若
单调递增,若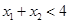 ,且
,且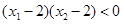 ,则
,则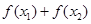 与0的大小关系是( )
与0的大小关系是( )
A.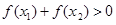 B.
B.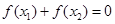
C.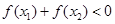 D.
D.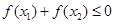
已知定义域为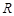 的函数
的函数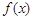 对任意实数
对任意实数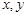 满足:
满足: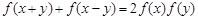 ,且
,且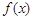 不是常值函数,常数
不是常值函数,常数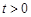 使
使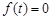 ,给出下列结论:①
,给出下列结论:①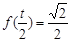 ;②
;②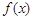 是奇函数;③
是奇函数;③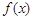 是周期函数且一个周期为
是周期函数且一个周期为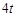 ;④
;④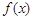 在
在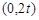 内为单调函数。其中正确命题的序号是___________。
内为单调函数。其中正确命题的序号是___________。
已知定义域为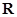 的函数
的函数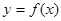 满足
满足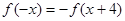 ,
当
,
当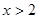 时,
时,
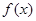 单调递增,若
单调递增,若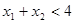 且
且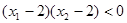 ,则
,则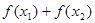 的值 ( )A.恒大于0 B.恒小于0 C.可能等于0 D.可正可负
的值 ( )A.恒大于0 B.恒小于0 C.可能等于0 D.可正可负
已知定义域为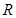 的函数
的函数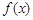 对任意实数
对任意实数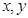 满足
满足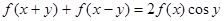 ,且
,且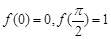 .给出下列结论:①
.给出下列结论:①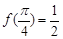 ,②
,②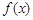 为奇函数,③
为奇函数,③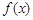 为周期函数,④
为周期函数,④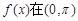 内单调递减.其中,正确的结论序号是
.
内单调递减.其中,正确的结论序号是
.
已知定义域为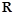 的函数
的函数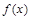 满足
满足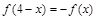 ,当
,当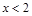 时,
时,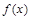 单调递减,如果
单调递减,如果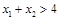 且
且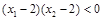 ,则
,则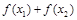 的值( )
的值( )
A.等于0 B.是不等于0的任何实数
C.恒大于0 D.恒小于0
1、A 2、C 3、B 4、D 5、A 6、D 7、C 8、B 9、A 10、D
11、 12、
13、或等 14、
15、(1), ----- (′)
(2)当时,,当时,,
由已知得,---------------------------------------------()
故当即时,----()
16、中:有两个不等的负根,,得,----()
中:无实根,得---()
命题与命题有且只有一个为真,
若真假,则,----------()
若假真,则,---------()
综上得-----------()
17、(1),由题意知,即, ∴,
得,
令得 ,或 (舍去)
当时,; 当时, ;
当时,有极小值,又
∴ 在上的最小值是,最大值是。----------()
(2)若在上是增函数,则对恒成立,
∴ , (当时,取最小值)。
∴ ---------------------------------()
18、(1)由题意可设,则,,
,点在函数的图像上,
,当时,,时,,
。-------------------------------------------------------------()
(2),
由对所有都成立得,,故最小的正整数。--()
19、(1)令得,令,得,
,为奇函数,
又,,在上是单调函数,故由 知在上是单调递增函数。------------------------------------------------------------------------------------()
(2)不等式即,由(1)知:,,即,
得-------------------------------------------------
(3)若对恒成立,
即对恒成立,
即对恒成立,
由在上是单调递增函数得
即对恒成立,
,得----------------------()
20、(1)数列是公比为的等比数列,且,
,数列隔项成等比,
-------------------------------------------------------------()
(2),当时,
,
当 时,,当时,
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com