
题目列表(包括答案和解析)
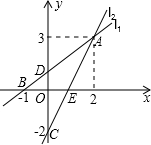 的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题:
的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题: 已知反比例函数y1=
已知反比例函数y1=| k |
| x |
| 1 |
| 2 |
 如图,直线l1的解析表达式为y=x+1,且l1与x轴交于点B(-1,0),与y轴交于点D.l2与y轴的交点为C(0,-3),直线l1、l2相交于点A(2,3),结合图象解答下列问题:
如图,直线l1的解析表达式为y=x+1,且l1与x轴交于点B(-1,0),与y轴交于点D.l2与y轴的交点为C(0,-3),直线l1、l2相交于点A(2,3),结合图象解答下列问题: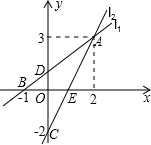 的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题:
的交点为C(0,-2),直线l1、l2相交于点A,结合图象解答下列问题: 如图,直线l1的解析表达式为y=x+1,且l1与x轴交于点B(-1,0),与y轴交于点D.l2与y轴的交点为C(0,-3),直线l1、l2相交于点A(2,3),结合图象解答下列问题:
如图,直线l1的解析表达式为y=x+1,且l1与x轴交于点B(-1,0),与y轴交于点D.l2与y轴的交点为C(0,-3),直线l1、l2相交于点A(2,3),结合图象解答下列问题:一、选择题(每小题2分,共20分)
1.A 2.D 3.D 4.B 5.C 6.B 7.A 8.D 9.B 10.C
二、填空题(每小题3分,共24分)
11. 12.
12. 13.9 14.(
13.9 14.( ) 15.2
) 15.2
16.2 17.50° 18.5
三、解答题
19.解:原式=
= ………………………………………………………………5分
………………………………………………………………5分
当 =-
=- 时,原式=
时,原式= =
= .………………………………………8分
.………………………………………8分
20.解:(1)解:∵∠AOB
=60°,OC平分∠BOA,∴
∵ PD∥OA, ∴ ∠DPO=∠AOC =30° ∴ DP=DO …………………… 3分
过点D作DE⊥OP于E,则OE= OP. …………………………………………… 5分
OP. …………………………………………… 5分
在Rr△DOE中, cos∠DOE=6×cos30°=
cos∠DOE=6×cos30°=  … 7分
… 7分
∴OP= . 即 OP的长为
. 即 OP的长为 cm. …………………………………… 8分
cm. …………………………………… 8分
21.解:(1) 中小奖(不超过50元)的概率为 . ……………… 2分
. ……………… 2分
(2)没有欺骗顾客.
因为
 (元)
(元)
所以平均奖金确实是180元. …………………………………………………4分
(3)10;10. ………………………………………………… 6分
“平均奖金180元”的说法不能反映中奖的一般金额.因为平均数容易受极端值的影响,在此问题中,用众数或中位数都能反映中奖的一般金额.…………………8分
22.(1)由题意知直线 交y轴于点D的坐标为(0,1),A点坐标为(2,3)
交y轴于点D的坐标为(0,1),A点坐标为(2,3)
∴ ∴
∴ ……………………………2分
……………………………2分
(2)设直线l 的一次函数的解析式为
的一次函数的解析式为
∵直线l 经过点A(2,3),点C(0,-2)
经过点A(2,3),点C(0,-2)
∴ 解得:
解得:
∴直线l 的一次函数的解析式为
的一次函数的解析式为 …………………………………………5分
…………………………………………5分
(3)∵ ,∴
,∴ ,
,
由图像知:当x>-1时直线 表示的一次函数的函数值大于0;当x>
表示的一次函数的函数值大于0;当x> 时直线
时直线 表示的一次函数的函数值大于0;…………………………………………………………7分
表示的一次函数的函数值大于0;…………………………………………………………7分
∴当x> 时直线
时直线 表示的一次函数的函数值大于0;……………………8分
表示的一次函数的函数值大于0;……………………8分
23.解:⑴相等⑵9 ,⑶9
,⑶9 ,…………………………………………………3分
,…………………………………………………3分
⑷△ADC的面积总等于△ABC的面积9 。…………………………4分
。…………………………4分
证明如下:
∵△ABC和△BDE都是等边三角形∴∠ACB=∠DBC=60°
∴BD∥AC,……………………………………………………………………6分
∴ (同底等高)∵
(同底等高)∵
∴△ADC的面积总等于△ABC的面积9 。…………………………………(8分)
。…………………………………(8分)
(5)画图略。………………………………………………………………………………10分
24.(1) 成立. ……………………………………………………1分
成立. ……………………………………………………1分
如图,延长CB到E,使BE=DN,连接AE。??????????????????????????????????????????????????????????? 2分
证明:∵AB=AD,∠ABE=∠D=90° ∴△ABE≌△AND………………………………3分
∴AE=AN, ∠BAE=∠NAD ………………………………………………………………4分
∵∠BAM+∠NAD=45° ∴∠BAM+∠BAE =45°即∠EAM=∠MAN =45°
∴ ……………………………………………………………………5分
……………………………………………………………………5分


 ????????????????????????????????????????? 6分
????????????????????????????????????????? 6分
(2) ???????????????????????????????????????????????????????????????????????????????????????????????? 7分
???????????????????????????????????????????????????????????????????????????????????????????????? 7分
证明略:方法同(1)………………………………………………………10分
25. (1) M(12,0),P(6,6). ……………………………………………………………4分
(2) 设此函数关系式为: . ……………………………………5分
. ……………………………………5分
∵函数 经过点(0,3),
经过点(0,3),
∴ ,即
,即 . ………………………………………………6分
. ………………………………………………6分
∴此函数解析式为: .……………………8分
.……………………8分
(3) 设A(m,0),则
B(12-m,0),C ,D
,D  . ………10分
. ………10分
∴“支撑架”总长AD+DC+CB =

=  . ………………………………………………………………………………………………11分
. ………………………………………………………………………………………………11分
∵ <0. ∴ 当m = 0时,AD+DC+CB有最大值为18. ………………………12分
<0. ∴ 当m = 0时,AD+DC+CB有最大值为18. ………………………12分
26.(1)由题意知:BD=5,BQ=t,QC=4-t,DP=t,BP=5-t
∵PQ⊥BC ∴△BPQ∽△BDC ∴ 即
即 ∴
∴
当 时,PQ⊥BC……………………………………………………………………3分
时,PQ⊥BC……………………………………………………………………3分
(2)过点P作PM⊥BC,垂足为M
∴△BPM∽△BDC ∴ ∴
∴ ……………………4分
……………………4分
∴
 =
= …………………………………………5分
…………………………………………5分
∴当 时,S有最大值
时,S有最大值 .……………………………………………………6分
.……………………………………………………6分
(3)①当BP=BQ时, , ∴
, ∴ ……………………………………7分
……………………………………7分
②当BQ=PQ时,作QE⊥BD,垂足为E,此时,BE=
∴△BQE∽△BDC ∴ 即
即 ∴
∴ ……………………9分
……………………9分
③当BP=PQ时,作PF⊥BC,垂足为F, 此时,BF=
∴△BPF∽△BDC ∴ 即
即 ∴
∴ ……………………11分
……………………11分
∴ ,
,  ,
, ,均使△PBQ为等腰三角形. …………………………12分
,均使△PBQ为等腰三角形. …………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com