如图甲所示，两平行金属板的板长l=0.20m，板间距d=6.0×10^－2m，在金属板右侧有一范围足够大的方向垂直于纸面向里的匀强磁场，其边界为MN，与金属板垂直。金属板的下极板接地，上极板的电压u随时间变化的图线如图乙所示，匀强磁场的磁感应强度B=1.0×10^－2T。现有带正电的粒子以v₀=5.0×10⁵m/s的速度沿两板间的中线OO´连续进入电场，经电场后射入磁场。已知带电粒子的比荷＝10⁸C/kg，粒子的重力忽略不计，假设在粒子通过电场区域的极短时间内极板间的电压可以看作不变，不计粒子间的作用（计算中取tan15°=4/15）。⑴求t＝0时刻进入的粒子，经边界MN射入磁场和射出磁场时两点间的距离；⑵求t＝0.30s时刻进入的粒子，在磁场中运动的时间；⑶试证明：在以上装置不变时，以v₀射入电场比荷相同的带电粒子，经边界MN射入磁场和射出磁场时两点间的距离都相等。

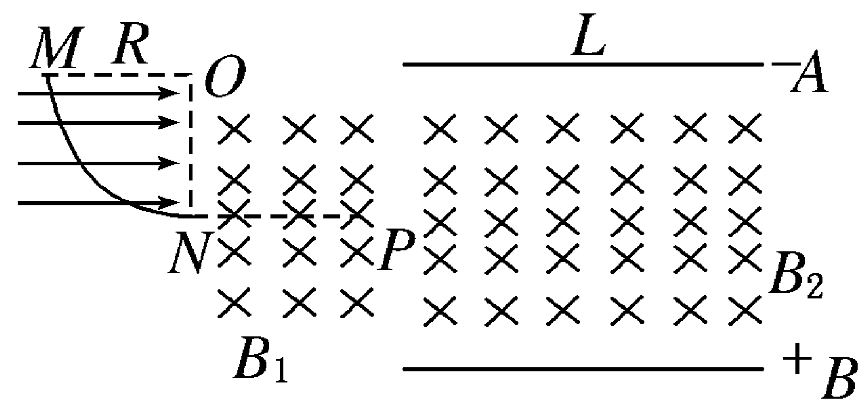
一正方形闭合导线框abcd，边长为L＝0.1m，各边的电阻均为0.1Ω，bc边位于x轴上且b点与坐标原点O重合。在x轴原点O的右侧有宽度0.2m、方向垂直纸面向里的匀强磁场区域，磁场的磁感强度为0.1T，如图2甲所示。当线框以4.0m/s的速度沿x轴匀速运动穿过磁场区域时，图乙中的图象表示的是线框从进入磁场到穿出磁场的过程中，线框的感应电流随位置变化的情况，其中正确的是

 

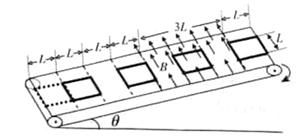
如图所示，线圈焊接车间的传送带不停地传送边长为L（L为未知量）质量为4 kg，电阻为5Ω的正方形单匝金属线圈，线圈与传送带之间的动摩擦系数。传送带总长8 L，与水平面的夹角为＝30⁰，始终以恒定速度2m/s匀速运动。在传送带的左端虚线位置将线圈无初速地放到传送带上，经过一段时间后线圈达到与传送带相同的速度。线圈运动到传送带右端掉入材料筐中（图中材料筐未画出）。已知当一个线圈刚好开始匀速运动时，下—个线圈恰好放到传送带上；线圈匀速运动时，相邻两个线圈的间隔也为L，线圈运动到传送带中点开始通过一固定的匀强磁场，磁感应强度为5T、磁场方向垂直传送带向上，匀强磁场区域宽度与传送带相同，沿传送带运动方向的长度为3L，重力加速度g=10m/s²。求：

(1)正方形线圈的边长L

(2)每个线圈通过磁场区域产生的热量Q

(3)在一个线圈通过磁场的过程,电动机对传送带做功的功率P