
题目列表(包括答案和解析)
如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,
轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() =1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。

如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,
轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() =1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
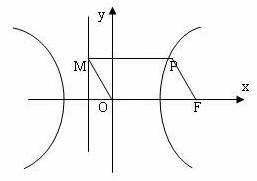
如图,F为双曲线C:![]() 的右焦点。P为双曲线C右支上一点,且位于
的右焦点。P为双曲线C右支上一点,且位于![]() 轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,
轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,![]() 。
。
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() =1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。
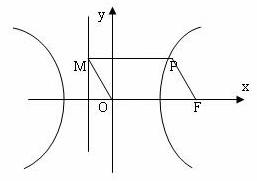
 的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,|PF|=λ|OF|,
的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为平行四边形,|PF|=λ|OF|,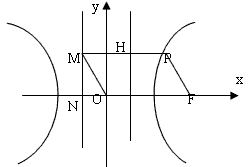
(Ⅰ)写出双曲线C的离心率![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)当![]() 时,经过焦点F且平行于OP的直线交双曲线于A、B点,若
时,经过焦点F且平行于OP的直线交双曲线于A、B点,若![]() ,求此时的双曲线方程。
,求此时的双曲线方程。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com