
题目列表(包括答案和解析)
(13分) 已知曲线C:![]() 的横坐标分别为1和
的横坐标分别为1和![]() ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且![]() ).设区间
).设区间![]() ,当
,当![]() 时,曲线C上存在点
时,曲线C上存在点![]() 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1) 证明:![]() 是等比数列;
是等比数列;
(2) 当![]()
![]()
![]() 对一切
对一切![]() 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3) 记数列{an}的前n项和为Sn,当![]() 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
(本小题满分14分)已知数列{an}中, (t>0且t≠1).若
(t>0且t≠1).若 是函数
是函数 的一个极值点.
的一个极值点.
(Ⅰ)证明数列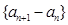 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记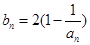 ,当t=2时,数列
,当t=2时,数列 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有
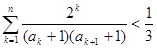 。
。
设定义域为R的函数f(x)满足下列条件:①对任意x∈R,f(x)+f(-x)=0;②对任意x∈[-1,1],都有![]() >0,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
>0,且f(-1)=-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立,则当a∈[-1,1]时,t的取值范围是( )
A.-2≤t≤2
B.t≤-![]() 或t=0或t≥
或t=0或t≥![]()
C.-![]() ≤t≤
≤t≤![]()
D.t≤-2或t=0或t≥2
已知曲线C:![]() 的横坐标分别为1和
的横坐标分别为1和![]() ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且![]() ).设区间
).设区间![]() ,当
,当![]() 时,曲线C上存在点
时,曲线C上存在点![]() 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
证明:![]() 是等比数列;
是等比数列;
当![]()
![]()
![]() 对一切
对一切![]() 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
记数列{an}的前n项和为Sn,当![]() 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
(本小题满分12分)
已知数列 满足
满足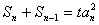 (t>0,n≥2),且
(t>0,n≥2),且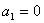 ,n≥2时,
,n≥2时, >0.其中
>0.其中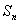 是数列
是数列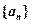 的前n项和.
的前n项和.
(Ⅰ)求数列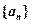 的通项公式;
的通项公式;
(Ⅱ)若对于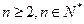 ,不等式
,不等式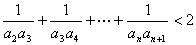 恒成立,求t 的取值范围.
恒成立,求t 的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com