
题目列表(包括答案和解析)
| N |
| n |
| N |
| n |
| N |
| n |
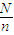 为整数时,
为整数时,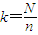 ;当
;当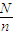 不是整数时,从 中剔除一些个体,使剩下的总体中的个体的个数N/能被n整除,这时k= ,并将剩下的总体重新编号;(3)在第一段采用简单随机抽样方法确定 个体编号l;(4)按照一定的规则抽取样本,通常将编号为l,l+k,l+2k,…l+(n-1)k
不是整数时,从 中剔除一些个体,使剩下的总体中的个体的个数N/能被n整除,这时k= ,并将剩下的总体重新编号;(3)在第一段采用简单随机抽样方法确定 个体编号l;(4)按照一定的规则抽取样本,通常将编号为l,l+k,l+2k,…l+(n-1)k| A.使用抽签法,每个个体被抽中的机会相等 | ||
B.使用系统抽样从容量为N的总体中抽取容量为n的样本,确定分段间隔k时,若
| ||
| C.分层抽样就是随意的将总体分成几部分 | ||
| D.无论采取怎样的抽样方法,必须尽可能保证样本的代表性 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com