如图所示是建筑工地上常用的一种“深穴打夯机”，电动机带动两个滚轮匀速转动将夯杆从深坑提上来，当夯杆底端刚到达坑口时，两个滚轮彼此分开，将夯杆释放，夯杆在自身重力作用下，落回深坑，夯实坑底，夯杆不反弹，设夯杆与坑底的接触时间为t=1.0s，然后两个滚轮再次压紧，将夯杆提上来，如此周而复始。已知两个滚轮边缘的线速度恒为v=4.0m/s，每个滚轮对夯杆的正压力均为F=2.0×10⁴N，滚轮与夯杆间的动摩擦因数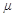=0.30，夯杆质量m=1.0×10³kg，坑深h=6.4m。假定在打夯的过程中坑的深度不变，g=10m／s²，求：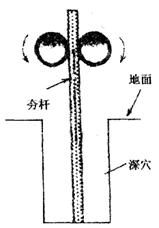

（1）从夯杆开始向上运动到刚开始匀速运动，夯杆上升的高度H是多少?
（2）每个打夯周期（从夯杆刚离开坑底到下一次夯杆刚离开坑底的时间）中，电动机对夯杆做的功W；
（3）打夯周期T。

如图所示是建筑工地上常用的一种“深穴打夯机”，电动机带动两个滚轮匀速转动将夯杆从深坑提上来，当夯杆底端刚到达坑口时，两个滚轮彼此分开，将夯杆释放，夯杆在自身重力作用下，落回深坑，夯实坑底，夯杆不反弹，设夯杆与坑底的接触时间为t=1.0s，然后两个滚轮再次压紧，将夯杆提上来，如此周而复始。已知两个滚轮边缘的线速度恒为v=4.0m/s，每个滚轮对夯杆的正压力均为F=2.0×10⁴N，滚轮与夯杆间的动摩擦因数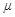=0.30，夯杆质量m=1.0×10³kg，坑深h=6.4m。假定在打夯的过程中坑的深度不变，g=10m／s²，求：

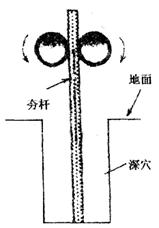
（1）从夯杆开始向上运动到刚开始匀速运动，夯杆上升的高度H是多少?

（2）每个打夯周期（从夯杆刚离开坑底到下一次夯杆刚离开坑底的时间）中，电动机对夯杆做的功W；

（3）打夯周期T。

如图所示，质量为m的小球放在光滑水平面上，在界线MN的左方始终受到水平恒力F₁作用，在MN的右方除受F₁外还受到与F₁在同一条直线上的水平恒力F₂的作用。小球从A点由静止开始运动，运动的v-t图像如图所示，由图可知下列说法中不正确的是（    ）

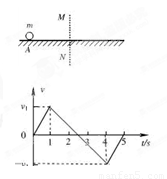
A . F₁与F₂的比值为1:2    

B. F₁与F₂的比值为3:5  

C. t=4. 0s时，小球经过界线MN              

D .小球向右运动的过程中, F₁与F₂做功的绝对值相等

如图所示，两条平行的金属导轨相距L=lm，水平部分处在竖直向下的匀强磁场B₁中，倾斜部分与水平方向的夹角为37°，处于垂直于斜面的匀强磁场B₂中，两部分磁场的大小均为0.5T。 金属棒MN和PQ的质量均为m=0.2kg，电阻分别为R_MN=0.5Ω和R_PQ=1.5Ω。MN置于水平导轨上，与水平导轨间的动摩擦因数μ=0.5，PQ置于光滑的倾斜导轨上，两根金属棒均与导轨垂直且接触良好。从t=0时刻起，MN棒在水平外力F₁的作用下由静止开始以a=2m/s²的加速度向右做匀加速直线运动，PQ则在平行于斜面方向的力F₂作用下保持静止状态。不计导轨的电阻，水平导轨足够长，MN始终在水平导轨上运动。求：

（1）t=5s时，PQ消耗的电功率；

（2）t=0～2.0s时间内通过PQ棒的电荷量；

（3）规定图示F₁、F₂方向作为力的正方向，分别求出F₁、F₂随时间t变化的函数关系；

（4）若改变F₁的作用规律，使MN棒的运动速度v与位移s满足关系：，PQ棒仍然静止在倾斜轨道上。求MN棒从静止开始到s=5m的过程中，F₁所做的功。