
题目列表(包括答案和解析)
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求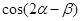 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴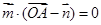 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,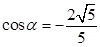 ,
,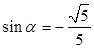 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即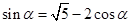 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)
表1:注射药物A后皮肤疱疹面积的频数分布表
|
疱疹面积 |
|
|
|
|
|
频数 |
30 |
40 |
20 |
10 |
|
频率/组距 |
|
|
|
|
表2:注射药物B后皮肤疱疹面积的频数分布表
|
疱疹面积 |
|
|
|
|
|
|
频数 |
10 |
25 |
20 |
30 |
15 |
|
频率/组距 |
|
|
|
|
|
(1) 完成上面两个表格及下面两个频率分布直方图;

(2)完成下面 列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”。 (结果保留4位有效数字)
|
|
疱疹面积小于70 |
疱疹面积不小于70 |
合计 |
|
注射药物A |
a= |
b= |
|
|
注射药物B |
c= |
d= |
|
|
合计 |
|
|
n= |
附:
|
P(K2≥k) |
0.10 |
0.05 |
0.025 |
0.010 |
0.001 |
|
k |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
 ;
;
【解析】根据已知条件,得到 列联表中的a,b,c,d的值,代入已知的公式中
列联表中的a,b,c,d的值,代入已知的公式中

然后求解值,判定两个分类变量的相关性。
解:
由于K2≥10.828,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”
欧拉(Euler),瑞士数学家及自然科学家.1707年4月15日出生于瑞士的巴塞尔,1783年9月18日于俄国彼得堡去逝.欧拉出生于牧师家庭,自幼受父亲的教育,13岁时入读巴塞尔大学,15岁大学毕业,16岁获硕士学位.
欧拉是18世纪数学界最杰出的人物之一,他不但为数学界做出了巨大的贡献,更把数学推至几乎整个物理的领域.他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学中的经典著作.
欧拉对数学符号的创立及推广起了积极的作用.比如用e表示自然对数的底,用i表示-1,用f(x)作为函数的符号,π虽不是欧拉首先提出的,但是在欧拉倡导下推广普及的.尤为不可思议的是欧拉将数学中最为活跃的五个数1,0,π,e,i竟用一个美妙绝伦的公式联系了起来:eiπ+1=0(欧拉指数公式),在西方数学界甚至认为此公式不亚于神的力量.
欧拉对数学的研究如此广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理.
1.你对欧拉(Euler)了解吗?请查阅欧拉(Euler)的故事,对于他“13岁时入读巴塞尔大学,15岁大学毕业,16岁获硕士学位”,你有何感触?
2.作为新时代的青年,你做好将来为科学事业做贡献的思想准备了吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com