练习册

  • 练习册
  • 试题
    20070206 (1)求p正确的m取值范围, (2)求p正确且q正确的m的取值范围. 【查看更多】

     

    题目列表(包括答案和解析)

    把一枚骰子抛6次，设正面出现的点数为x，

    （1）求出x的可能取值情况（即全体基本事件）；

    （2）下列事件由哪些基本事件组成（用x的取值回答）.

    ①x的取值为2的倍数（记为事件A）；

    ②x的取值大于3（记为事件B）；

    ③x的取值不超过2（记为事件C）；

    ④x的取值是质数（记为事件D）.

    （3）判断上述事件是否为古典概型，并求出其概率.

    查看答案和解析>>

    把一枚骰子抛6次，设正面出现的点数为x，

    （1）求出x的可能取值情况（即全体基本事件）；

    （2）下列事件由哪些基本事件组成（用x的取值回答）.

    ①x的取值为2的倍数（记为事件A）；

    ②x的取值大于3（记为事件B）；

    ③x的取值不超过2（记为事件C）；

    ④x的取值是质数（记为事件D）.

    （3）判断上述事件是否为古典概型，并求出其概率.

    查看答案和解析>>

    已知A（-5，0），B（5，0），动点P满足|
    PB
    |，
    1
    2
    |
    PA
    |，8成等差数列．
    （1）求P点的轨迹方程；
    （2）对于x轴上的点M，若满足|
    PA
    |•|
    PB
    |=
    PM
    2    ，则称点M为点P对应的“比例点”．问：对任意一个确定的点P，它总能对应几个“比例点”？

    查看答案和解析>>

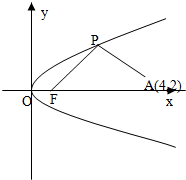    精英家教网如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
    （1）求|PA|+|PF|的最小值；
    （2）求k的取值范围；
    （3）若O为坐标原点，问是否存在点M，使过点M的动直线与抛物线交于B，C两点，且以BC为直径的圆恰过坐标原点，若存在，求出动点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    已知向量
    a
    =(m，n)，
    b
    =(sinx，1)，
    c
    =(cosx，sinx)，
    a
    •
    b
    ∈[-7，1]
    （1）求
    a
    •
    c
    的最大值；
    （2）若m＞0，向量
    OP
    =
    a
    +
    c
    ，求点P（x，y）的轨迹方程及|
    a
    +
    c
    |    的最大值．

    查看答案和解析>>

     

    一、选择题

    1．A    2．B    3．D    4．B    5．B    6．B    7．C    8．A    9．C

    10．B   11．B   12．C

    二、填空题

    13．                 －3

    14．

    15．2

    16．

    三、解答题

    17．解：原不等式可化为

    即

    ………………………………6分

    当…………8分

    当…………10分

    当…………12分

    18．解：

    ………………6分

       （1）函数的最小正周期…………8分

       （2）

    取得最大值.

    最大值为………………12分

    19．解：

       （1）甲恰好投中2次的概率为………………3分

       （2）乙至少投中2次的概率为…………7分

       （3）设甲、乙两人共投中5次为事件A，甲恰好投中3次且乙恰投中2次为事件B1，甲恰投中2次且乙恰好投中3次为事件B2，则A=B1+B2，B1，B2为互斥事件.

    ………………9分

    ………………11分

    所以，甲、乙两人共投中5次的概率为 ………………12分

    20．解：

       （1）

    解得（舍去）…………5分

       （2）假设存在a，b使得

    即

    …………9分

    对于一切自然数

    解得……………………12分

    21．解：

       （1）设椭圆方程为，则

    ，

    由题意得………………4分

    故椭圆方程为………………6分

       （2）设，

    …………10分

    当取到最大值，此时最大，故的最大为………………12分

    22．解：由题设x1和x2是方程.

    所以

    当………………3分

    由题意，不等式对于任意实数恒成立的m的解集等价于不等式3的解集，由此不等式得

      ①

    或②………………6分

    不等式①的解为不等式②的解集为

    因此，当时，P是正确的…………7分

    对函数，求导得

    令

    此一元二次方程的判别式

    若的符号如下

    x

    +

    0

    +

    因此，的根植.

    若的符号如下

    x

    （）

    +

    0

    －

    0

    +

    因此，函数处取得极大值，在处取得极小值

    综上述，当且仅当上有极值…………12分

    由是正确的.

    综上，使p正确且q正确时，实数m的取值范围是

    …………………………14分


    同步练习册答案