练习册

  • 练习册
  • 试题
    已知函数f(x)＝x4+ax3+2x2+b.其中a.b∈R.的单调递增区间,仅在x＝0处有极值.求a的取值范围,(3)若对于任意的a∈[-2,2].不等式f(x)≤1在x∈[ -1,1]上恒成立.求b的取值范围. 抚州市2009届高三统一考试数学试题(文) 【查看更多】

     

    题目列表(包括答案和解析)

    （2011•广东模拟）（本小题满分14分 已知函数f(x)=
    		3
    sin2x+2sin(
    π
    4
    +x)cos(
    π
    4
    +x)    ．
    （I）化简f（x）的表达式，并求f（x）的最小正周期；
    （II）当x∈[0，
    π
    2
    ]  时，求函数f(x)    的值域．

    查看答案和解析>>

    ．(本小题满分14分)已知函数f (x)=lnx，g(x)=ex．

    ( I)若函数φ (x) = f (x)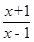－，求函数φ (x)的单调区间；

    (Ⅱ)设直线l为函数的图象上一点A(x0，f (x0))处的切线．证明：在区间(1，+∞)上存在唯一的x0，使得直线l与曲线y=g(x)相切．

     

     

    查看答案和解析>>

    (本小题满分14分)

    已知函数f(x)=2sin2(+x)-cos2x．

    (1)求f(x)的值域；

    (2)求f(x)的周期及单调递减区间．

     

     

    查看答案和解析>>

     (本小题满分14分)

    已知函数f (x)=ex，g(x)=lnx，h(x)=kx+b.

    (1)当b=0时，若对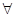x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；

    (2)设h(x)的图象为函数f (x)和g(x)图象的公共切线，切点分别为(x1, f (x1))和(x2, g(x2))，其中x1>0.

    ①求证：x1>1>x2；

    ②若当x≥x1时，关于x的不等式ax2－x+xe+1≤0恒成立，求实数a的取值范围.

     

    查看答案和解析>>

    (本小题满分14分)

    已知函数f(x)=log2.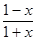

    （1）判断并证明f(x)的奇偶性;

    （2）若关于x的方程f(x)=log2(x-k)有实根，求实数k的取值范围;

    （3）问：方程f(x)=x+1是否有实根？如果有，设为x0，请求出一个长度

    为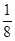的区间(a,b)，使x0∈(a,b)；如果没有，请说明理由.

    （注：区间(a,b)的长度为b-a）

     

    查看答案和解析>>

    1.A　2.B　3.A　4.C　5.C　6.B　7.D　8.B　9.B　10.D　11.B　12.D

    13.－3　14.7　15.②④　16.3

    17.解：(1)f(x)＝Acos2(ωx＋φ)＋1＝cos(2ωx＋2φ)＋＋1.

    又A＞0，ω＞0,0＜φ＜，∴f(x)的最大值为A＋1，最小值为1.

    由f(x)的最大值与最小值的差为2，∴A＝2.

    由f(x)过点(0,2)，f(0)＝cos 2φ＋2＝2，∴φ＝，

    则T＝4π＝，∴ω＝，f(x)＝cos(x＋)＋2＝2－sinx.6分

    (2)∵B＝，∴b＝f(B)＝2－sin(?)＝.

    设A，C所对的边分别为a，c，由余弦定理得＝a2＋c2－2accos，＋ac＝a2＋c2≥2ac，ac≤，

    当且仅当a＝c＝时等号成立，△ABC的面积S＝acsin≤.12分

    18.解：(1)某应聘者能被聘用的概率为p0＝1－(1－)(1－)(1－p)＝＋p.4分

    (2)在4位应聘者中恰好有2人被聘用的概率为CP?(1－P0)2，

    恰有3位被聘用的概率为Cp?(1－p0)1，依题意Cp?(1－p0)2≥Cp?(1－p0)1，解得p0≤，

    即＋p≤⇒0≤p≤.12分

    19.解：(1)连AQ，∠PQA是PQ与平面ABCD所成角，AQ＝2，BQ＝2，即Q是BC的中点，过Q作QH⊥AD于H，则QH⊥平面PAD，过Q作QM⊥PD，连MH，则∠QMH为所求二面角的平面角.

    在Rt△PAD中，＝⇒MH＝＝＝，

    所以tan∠QMH＝＝＝，

    从而所求二面角的大小为arctan .6分

    (2)由于Q是BC的中点，可得DQ⊥PQ，

    ⇒面PAQ⊥面PDQ，

    过A作AG⊥PQ于G，则AG为点A到平面PQD的距离.

    AG＝＝＝.12分

    另解：分别以AD，AB，AP为x，y，z轴建立空间直角坐标系，

    由条件知Q是BC的中点，面PAD的一个法向量是＝(0,2,0).

    又D(4,0,0)，Q(2,2,0)，P(0,0,4)，

    故＝(0,2,0)，＝(－4,0,4)，

     

    设面PDQ的法向量为n＝(x，y，z)，

    则⇒由此可取n＝(1,1,1)，

    从而(1)cos〈，n〉＝＝＝.

    (2)面PDQ的一个法向量为n＝(1,1,1)，＝(2,2,0)，

    故点A到平面PDQ的距离d＝＝＝.

    20.解：(1)an＋1＝an－1＋(－1)n－1＋n，于是a3＝a1＋2－1＝2，a2n－1＝a2n－3－1＋2n－2(n≥2)，

    ∴a2n－1＝a2n－3＋2n－3(n≥2).

    …………

    a3＝a1＋1

    a2n－1＝a1＋＝n2－2n＋2.2分

    而a2＝b1＋1＝2

    a4＝b3＋3＝a2＋4

    …………

    a2n＝a2n－2＋2n

    ∴a2n＝a2n－2＋2n

    ∴a2n＝a2＋＝n2＋n.8分

    (2)Sn＝＋＋…＋

    ＝＋＋…＋＝1－

    ∴S2009＝1－＝.12分

    21.解：(1)设P(x，y)，则＝(－2－x，－y)，＝(2－x，－y)，依题意有(－2－x)(2－x)＋y2＝?，化简得x2－y2＝2.4分

    (2)假设存在定点F(m,0)，使?为常数.

    当直线l与x轴不垂直时，设l：y＝k(x－2)，

    ⇒(1－k2)x2＋4k2x－4k2－2＝0，

    依题意k2≠1，设M(x1，y1)，N(x2，y2)，则

    于是?＝(x1－m，y1)(x2－m，y2)＝(k2＋1)x1x2－(2k2＋m)(x1＋x2)＋4k2＋m2

    ＝＋m2－4m＋2.8分

    要使?是与k无关的常数，当且仅当m＝1，此时?＝－1.

    当直线l⊥x轴时，可得M(2，)，N(2，－)，若m＝1，则?＝(1，)(1，－)＝－1.

    所以在x轴上存在定点F(1,0)，使?为常数.12分

    22.解：f′(x)＝4x3＋3ax2＋4x＝x(4x2＋3ax＋4).

    (1)当a＝－时，f′(x)＝4x3＋3ax2＋4x＝2x(2x－1)(x－2)，令f′(x)≥0，得0≤x≤或x≥2，所以f(x)的增区间为[0，]与[2，＋∞).4分

    (2)f′(x)＝x(4x2＋3ax＋4)，显然x＝0不是方程4x2＋3ax＋4＝0的根，为使f(x)仅在x＝0处有极值，4x2＋3ax＋4≥0必须恒成立，即有Δ＝9a3－64≤0，解得a∈[－，].8分

    (3)由条件a∈[－2,2]知Δ＝9a2－64＜0，从而4x2＋3ax＋4＞0恒成立.

    当x＜0时f′(x)＜0；当x＞0时，f′(x)＞0.

    因此f(x)在区间[－1,1]上的最大值为max{f(－1)，f(1)}.

    为使对任意a∈[－2,2]，f(x)≤1在x∈[－1,1]上恒成立，当且仅当⇒在a∈[－2,2]上恒成立，解得b≤－4，故b的取值范围是(－∞，－4].

     

     


    同步练习册答案