练习册

  • 练习册
  • 试题
    (本小题满分8分,每小题4分)设复数z=. 【查看更多】

     

    题目列表(包括答案和解析)


    （本小题满分12分）
    某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验.选取两大块地，每大块地分成n小块地，在总共2n小块地中，随机选n小块地种植品种甲，另外n小块地种植品种乙.
    （I）假设n=4，在第一大块地中，种植品种甲的小块地的数目记为X，求X的分布列和数学期望；
    （II）试验时每大块地分成8小块，即n=8，试验结束后得到品种甲和品种乙在个小块地上的每公顷产量（单位：kg/hm2）如下表：

    分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种？
    附：样本数据x1，x2，…，xa的样本方差，其中为样本平均数.

    查看答案和解析>>

    （本小题满分13分）（Ⅰ）小问5分，（Ⅱ）小问8分）

    某市公租房的房源位于A，B，C三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的求该市的任4位申请人中：

       （Ⅰ）恰有2人申请A片区房源的概率；

       （Ⅱ）申请的房源所在片区的个数的分布列与期望

    查看答案和解析>>

     （本小题满分13分，（Ⅰ）小问5分，（Ⅱ）小问8分．）

    卫生部门对某大学的4个学生食堂进行食品卫生检查（简称检查）.若检查不合格，则必须整改，若整改后经复查不合格则强行关闭该食堂.设每个食堂检查是否合格是相互独立的，且每个食堂整改前检查合格的概率为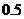，整改后检查合格的概率是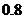.计算（结果用小数表示，精确到）

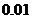    （Ⅰ）恰有一个食堂必须整改的概率；

    （Ⅱ）至少关闭一个食堂的概率.

     

     

     

     

     

     

    查看答案和解析>>

    (本题满分18分) 本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.

    设，对于项数为的有穷数列，令为中最大值，称数列为的“创新数列”．例如数列3，5，4，7的创新数列为3，5，5，7．

    考查自然数的所有排列，将每种排列都视为一个有穷数列．

    （1）若，写出创新数列为3，4，4，4的所有数列；

    （2）是否存在数列的创新数列为等比数列？若存在，求出符合条件的创新数列；若不存在，请说明理由．

    （3）是否存在数列，使它的创新数列为等差数列？若存在，求出满足所有条件的数列的个数；若不存在，请说明理由．

     

    查看答案和解析>>

     （本题是选做题，满分28分，请在下面四个题目中选两个作答，每小题14分，多做按前两题给分）

    A．(选修4-1：几何证明选讲)

    如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE＝PA，，PD＝1，BD＝8，求线段BC的长.

     

     

     

     

     

     

    B．(选修4-2：矩阵与变换)

    在直角坐标系中，已知椭圆，矩阵阵，，求在矩阵作用下变换所得到的图形的面积.

    C．(选修4-4：坐标系与参数方程)

    直线(为参数，为常数且)被以原点为极点，轴的正半轴为极轴，方程为的曲线所截，求截得的弦长.

    D．(选修4-5：不等式选讲)

    设，求证：.

     

     

     

     

     

    查看答案和解析>>

    YC一、选择题：CDBBA，  CBDDB，  DB 

    二、填空题：13． ；  14．3   15．76   16．（1，e）；e

    三、解答题：

    17．解：（1）f‘（x）=-3x2+6x+9                        …………2分

       令 f‘（x）<0，解得x<-1或x>3。                   …………4分

       *函数f（x）的单调递减区间为（-。   …………5分

    （2）f（－2）=2+a ，     f（2）=22+a

      f（2）>f（―2）

    在（―1，3）上f‘（x）>0    f（x）在[―1，2]上单调递增。

    又f（x）在[―2，1]上单调递减。              …………8分

    ∴f2）和f（-1）分别是f（x）在[―2，2]上的最大值和最小值。

    于是有  22+a=20 ， 解得a=-2

    故f（x）=―x3+3x2+9x-2                        …………10分

     

    ∴f（-1）=-7

    即f（x）在[―2，2]上的最小值为-7 。         …………12分

    18. 用表示一天之内第个部件需要调整的事件，，则，                ……………………1分

        以表示一天之内需要调整的部件数，则

      （Ⅰ）……4分

      （Ⅱ）………7分

      （Ⅲ）              ……………………8分

        …………9分

                         ……………………10分

    的分布列为

    0

    1

    2

    3

    p

    0.504

    0.398

    0.092

    0.006

      …………12分

    19．（本小题满分12分）

    解: (I)法一：取CC1的中点F, 连接AF, BF, 则AF∥C1D．

    ∠BAF为异面直线AB与C1D所成的角或其补角．……(1分)

    ∵△ABC为等腰直角三角形,

    AC＝2, ∴AB＝2．又∵CC1＝2, ∴AF＝BF＝．

    ∵∴

    ∴即异面直线AB与C1D所成的角为(4分)

    法二：以C为坐标原点，CB，CA，CC1分别为x轴，y轴，z轴建立空间直角坐标系，则A（0，2，0），B（2，0，0），C1（0，0，2），D（0，2，1），∴=（2，－2，0），=（0，2，－1）.

    由于异面直线AB与C1D所成的角为向量与的夹角或其补角.……（1分）

    设与的夹角为θ，

    ，即异面直线AB与C1D

    所成的角为…………（4分）

     

     

     

     

     

     

     

     

    在三棱锥D―B1C1E中，

    点C1到平面DB1E的距离为，

    B1E＝, DE＝, 又B1E⊥DE,

    ∴△DB1E的面积为

    ∴三棱锥C1―DB1E的体积为1．

    …………(10分)

    设点D到平面的距离为d,

    在△中, B1C1＝2, B1E＝C1E＝,

    ∴△B1C1E的面积为．

    由得, 即点D到平面的距离为．………(12分)

     

    20．解：（I）由已知得：a2=  ，a3=   a4= 。        …………4分

    （2）猜想a=。                                 …………6分

    下面用数学归纳法证明：略。                             …………12分

    21．本小题满分14分

        解：（I）设该学生从家出发，先乘船渡河到达公路上某一点P(x,0) (0≤x≤d)，再乘公交车去学校，所用的时间为t，则.……3分

            令……………………………………………………5分

            且当…………………………………………………6分

            当……………………………………………………7分

            当时，所用的时间最短，最短时间为：

    .………………………………9分

    答：当d=2a时，该学生从家出发到达学校所用的最短时间是.

    （II）由（I）的讨论可知，当d=上的减函数，所以当时，

    即该学生直接乘船渡河到达公路上学校，所用的时间最短.……………………12分

    最短的时间为………………………………………………14分

    答：当时，该学生从家出发到达学校所用的最短时间是.

    22．（1），由已知在[0，1]上大于等于0，在[1，2]上小于等于0.∴x=1为极大值点，

          …………4分

       （2）由，有三个相异实根，

    且                       …………8分

       （3）在[1，2]上为减函数，∴最大值为，∴只有上恒成立即可

    恒成立，又，

    的最大值为－2，                    …………12分

     

     

     


    同步练习册答案