题目列表(包括答案和解析)
如图所示，两个相同的小球质量均为m＝0.2 kg，用长L＝0.22 m的细绳连接，放在倾角为30°的足够长的光滑斜面上，初始时刻，细绳拉直，且与斜面底边平行．在绳的中点O作用一个垂直于绳、沿斜面向上的恒力，大小F＝2.2 N．在F的作用下两小球沿斜面向上运动，经过一段时间两小球第一次碰撞，又经过一段时间第二次发生碰撞……．每一次碰撞后，小球垂直于F方向的速度都比碰撞前减小．当力F作用了2 s时，两小球发生最后一次碰撞，且碰后不再分开．取g＝10 m/s2，求：
(1)最后一次碰撞后，小球的加速度．
(2)最后一次碰撞后，小球的最小速度．
(3)整个过程中，系统由于碰撞而损失的机械能．
如图所示，两个完全相同的光滑球的质量均为m，放在竖直挡板和倾角为α的固定斜面间．若缓慢转动挡板至与斜面垂直，在此过程中（ ）
两个相同的小球A和B，质量均为m，用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O，并用长度相同的细线连接A、B两小球，然后，用一水平方向的力F作用在小球A上，此时三根细线均处于直线状态，且OB细线恰好处于竖直方向，如图所示．如果不考虑小球的大小，两小球均处于静止状态，则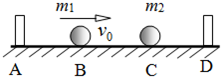
如图所示，两个不计厚度的弹性挡板分别固定在水平桌面上A、D的位置，两个大小相同可看作质点的小球质量分别为m1、m2，且m2=5m1，开始时两球位于B、C的位置，且AB=BC=CD=L，m2静止，m1以水平初速度v0向m2运动，设两球之间、球与挡板之间的碰撞均没有机械能损失，碰撞时间、所有摩擦均不计．求
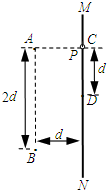如图所示，两个带等量异种电荷的点电荷，电荷量均为 Q，固定于同一条竖直线上的 A、B 两点处，其中 A 处的电荷带正电，B 处的电荷带负电，A、B 相距为2d．MN 是竖直放置的光滑绝缘细杆，另有一个穿过细杆的带电小球 P，质量为 m、电荷量为+q （可视为点电荷），现将小球 P 从与点电荷 A 等高的 C 处由静止释放，小球 P 向下运动到与 C点距离为 d 的 D 点时，速度为 v．已知 MN 与 AB 之间的距离为 d，静电力常量为 k，重力加速度为 g，若取无限远处的电势为零，试求：一:不定项选择题（本题共8小题，每题6分，共48分 ）
题号
1
2
3
4
5
6
7
8
答案
B
CD
BD
ABC
AD
AC
B
AD
9.(1) C （5分）(2) ① 如右图所示( 7分 )
② 
（
5分 ）
( 注意：电路图中，如有一个地方不对，不能得分 )
10、解：(1)ab棒达到稳定速度后，应具有受力平衡的特点，设此时棒ab所受安培力为FB.则F-mgsin30°+FB ① （ 2分 ）
而FB=BIL=
② （ 1分 ） 牵引力 F=
③ （ 1分 ）
将②③代人①后得 =mgsin30°+ （ 1分 ）
代人数据后得v1=
(2)设从静止到稳定速度所需时间为t.棒ab从静止开始到具有稳定速度的过程中在做变加速直线运动，据能量关系有：Pt-mgsin30°?s―Q=
-0（7分）
代人数据得t=1.5s.（2分）
11、解：（1）平板车和小物块组成的系统水平方向动量守恒，故小物块到达圆弧最高点A时，二者的共同速度
（ 1分 ） 设弹簧解除锁定前的弹性势能为
，上述过程中系统能量守恒，则有 
（ 4分 ）
代入数据解得 
（ 1分 ）
（2）设小物块第二次经过
时的速度大小为
，此时平板车的速度大小为
，研究小物块在平板车圆弧面上的下滑过程，由系统动量守恒和机械能守恒有
（ 2分 ） 
（ 3分 ）
由式代入数据解得 
（ 1分 ）
（3）最终平板车和小物块相对静止时，二者的共同速度为0。（1分）
设小物块相对平板车滑动的路程为S，对系统由能量守恒有 
（4分）
代入数据解得
（ 1分 ）
则距点的距离
（ 1分 ）
12、解:（1）设沿斜面向上为正方向．
由牛顿第二定律：
（ 3分 ）
解得 
（
2分 ）
（2）由分析可知:对两小球和绳组成的整体，两小球沿斜面向上的方向上，
由牛顿第二定律：得a＝
最后一次碰撞后，小球的最小速度为v＝at＝0.5×
（3）2s内，小球沿斜面向上的位移为 
（
2分 ）
设整个过程中，系统由于碰撞而损失的机械能为E ，
由功能关系：
（
5分 ）
解得
（ 2分 ）
（ 注：计算题如按其它方法，答案正确，同样得分 ）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com