
题目列表(包括答案和解析)
 图中的曲线是
图中的曲线是![]()
![]() 的图象,已知
的图象,已知![]() 的值为
的值为![]() ,
,![]() ,
,![]() ,
,![]() ,则相应曲线
,则相应曲线![]() 的
的![]() 依次为 ( )
依次为 ( )
A.![]() ,
,![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]() ,
,![]()
曲线C1、C2、C3、C4分别是指数函数y=ax,y=bx,y=cx和y=dx的图象,则a、b、c、d与1的大小关系是
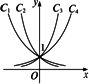
a<b<1<c<d
a<b<1<d<c
b<a<1<c<d
b<a<1<d<c
 图中曲线是幂函数y=xn在第一象限的图像,已知n可取±2,±
图中曲线是幂函数y=xn在第一象限的图像,已知n可取±2,±![]() 四个值,则相应于曲线
四个值,则相应于曲线![]() 的n依次为( )
的n依次为( )
A.-2,-![]() ,
,![]() ,2 B.2,
,2 B.2,![]() ,-
,-![]() ,-2
,-2
C. -![]() ,-2,2,
,-2,2,![]() D. 2,
D. 2,![]() ,-2, -
,-2, -![]()
图中曲线是幂函数y=xn在第一象限的图象,已知n取±3,± 四个值,则相应于曲线C1,C2,C3,C4的n依次为 ( )
四个值,则相应于曲线C1,C2,C3,C4的n依次为 ( )

A.-3,- ,
, ,3 B.3,
,3 B.3, ,-
,- ,-3
,-3
C.- ,-3,3,
,-3,3, D.3,
D.3, ,-3,-
,-3,-
函数的图象与方程的曲线有着密切的联系,如把抛物线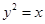 的图象绕原点沿逆时针方向旋转
的图象绕原点沿逆时针方向旋转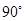 就得到函数
就得到函数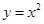 的图象.若把双曲线
的图象.若把双曲线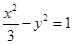 绕原点按逆时针方向旋转一定角度
绕原点按逆时针方向旋转一定角度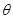 后,能得到某一个函数的图象,则旋转角
后,能得到某一个函数的图象,则旋转角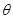 可以是( )
可以是( )
A. B.
B.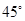 C.
C.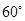 D.
D.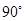
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
A
D
B
C
C
D
D
A
C
二、填空题
13. 14.
14. 15.4 16.③④
15.4 16.③④
三、解答题
17.解:(1) ,
,
 (2分)
(2分)
又 (4分)
(4分)
 . (6分)
. (6分)
(2)
 (8分)
(8分)

 (10分)
(10分)
 18.(1)证明:连结
18.(1)证明:连结 交
交 于点
于点 ,取
,取 的中点
的中点 ,连结
,连结 ,则
,则 //
//  且
且 依题意,知
依题意,知 且
且 ,
,
 ,且
,且 ,
,
故四边形 是平行四边形,
是平行四边形,
 ,即
,即 (3分)
(3分)
又 平面
平面 ,
, 平面
平面
 平面
平面 , (6分)
, (6分)
(2)解:处长 交
交 的处长线于
的处长线于 点,连结
点,连结 ,作
,作 于
于 ,连结
,连结 .
.
∵平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面 ,
,
由三垂线定理,知 ,故
,故 就是三面角
就是三面角 的平面角.(8分)
的平面角.(8分)
∵平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面 ,故
,故 就是直线
就是直线 与平面
与平面 成的角, (10分)
成的角, (10分)
知 设
设 ,则
,则 .
.
在直三角形 中:
中:


 .
.
在直角三角形 中:
中:
故三而角 的大小为60°. (12分)
的大小为60°. (12分)
19.解:(1)记 表示事无偿援助,“取出的2件产品中无二等品”,
表示事无偿援助,“取出的2件产品中无二等品”,
 表示事件“取出的2件产品中恰有1件是二等品”。则
表示事件“取出的2件产品中恰有1件是二等品”。则 、
、 互斥,且
互斥,且
故
依题意,知 又
又 ,得
,得 (6分)
(6分)
(2)(理) 可能的取值为0,1,2,
可能的取值为0,1,2,
若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件,故
 (9分)
(9分)

0
1
2




所以 的分布列为
的分布列为
∴ 的期望
的期望 (12分)
(12分)
20.解:(1) 在
在 上单调递增,
上单调递增, 上单调递减,
上单调递减,
 有两根
有两根 ,2,
,2,
 (4分)
(4分)
今 则
则
因为 在
在 上恒大于0,
上恒大于0,
所以 在
在 上单调递增,故
上单调递增,故
 (6分)
(6分)
(2)

 (8分)
(8分)
①当 时,
时, ,定义域为
,定义域为
 恒成立,
恒成立, 在
在 上单调递增; (9分)
上单调递增; (9分)
②当 时,
时, ,定义域:
,定义域:
 恒成立,
恒成立, 在
在 上单调递增; (10分)
上单调递增; (10分)
③当 时,
时,  ,定义域:
,定义域:
由 得
得 ,由
,由 得
得 .
.
故在 上单调递增;在
上单调递增;在 上单调递减. (11分)
上单调递减. (11分)
所以当 时,
时, 在
在 上单调递增,故
上单调递增,故 无极值;
无极值;
当 时,
时, 在
在 上单增;故
上单增;故 无极值.
无极值.
当 时,
时, 在
在 上单调递增;在
上单调递增;在 上单调递减.
上单调递减.
故 有极小值,且
有极小值,且 的极小值
的极小值 . (12分)
. (12分)
21.解:(1)设 依题意得
依题意得
 (2分)
(2分)
消去 ,
, ,整理得
,整理得 . (4分)
. (4分)
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示圆. (6分)
时,方程表示圆. (6分)
(2)当 时,方程为
时,方程为 设直线
设直线 的方程为
的方程为
 (8分)
(8分)
消去 得
得 (10分)
(10分)
根据已知可得 ,故有
,故有
 直线
直线 的斜率为
的斜率为 (12分)
(12分)
22.证明:(1)即证

 (2分)
(2分)
假设 则
则
 (4分)
(4分)


综上所述,根据数学归纳法,命题成立 (6分)
(2)由(1),得
 (8分)
(8分)
 (10分)
(10分)
又 即
即 (12分)
(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com