练习册

  • 练习册
  • 试题
    求与平面所成的角． 【查看更多】

     

    题目列表(包括答案和解析)

    AB与平面α所成的角为1，AC在平面α内，AC和AB在α内的射影AB1所成的角为2，设∠BAC＝．

    求证：cos＝cos1cos2．

    查看答案和解析>>

    平面直角坐标系x0y中，动点P到直线x=-2的距离比它到点F（1，0）的距离大1．
    （1）求动点P的轨迹C；
    （2）求曲线C与直线x=4所围成的区域的面积．

    查看答案和解析>>

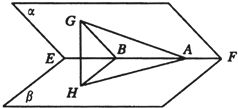    平面角为锐角的二面角α-EF-β，A∈EF，AG?α，∠GAE=45°，若AG与β所成角为30°，求二面角α-EF-β的平面角．

    查看答案和解析>>

    平面直角坐标系x0y中，动点P到直线x＝－2的距离比它到点F(1，0)的距离大1．

    (1)求动点P的轨迹C；

    (2)求曲线C与直线x＝4所围成的区域的面积．

    查看答案和解析>>

    设平面向量
    a
    =(m，1)    ，
    b
    =(2，n)    ．
    （I）当m，n∈{-2，-1，1，2}时．记“
    a
    ⊥
    b
    ”为事件A，求事件A发生的概率；
    （II）当m∈[-1，2]，n∈[-1，1]时，记“
    a
    与
    b
    所成角为钝角”为事件B，求事件B发生的概率．

    查看答案和解析>>

    一、选择题：本大题共10小题，每小题5分，共50分．

     

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    A

    D

    C

    B

    D

    A

    B

    B

    C

    D

     

    二、填空题：本大题7小题，每小题4分，共28分．

    11、； 12、 ； 13、；  14、； 15、；  16、 ；17、或。

    三、解答题

    18、（1）略   …………………………………………………………………………（7分）

    （2）  …………………………………………………………（14分）

    19、（1）tanA=     …………………（7分）

    (2) 原式=

    =   ……………………………………………………………………（14分）

    20、（1）略      ……………………………………………………………………（7分）

    （2）就是二面角的平面角，即，

     …………………………………………………………………（9分） 

     取中点，则平面，

    就是与平面所成的角。   …………………………（11分）

    ，，

    所以与平面所成的角的大小为。 …………………………（14分）

    （用向量方法，相应给分）

    21、（1），

             又在区间（－∞，0）及（4，+∞）上都是增函数，在区间（0，4）上是减函数，      又．………（6分）

       （2）

             当点是切点时，切线方程为9x+6y－16=0．………………（10分）

    当点不是切点时，切点为，

    得     所以切点为，

    切线方程为．……………………………………（14分）

    22、解：解：（1）、设，则，

     ∵点P分所成的比为   ∴    ∴  

    ∴     代入中，得 为P点的轨迹方程．

    当时，轨迹是圆． …………………………………………………（8分）

    （2）、由题设知直线l的方程为， 设

    联立方程组  ，消去得：　

    ∵ 方程组有两解  ∴ 且  ∴或且    

       ∵

          ∴    

    又 ∵    ∴    解得（舍去）或

    ∴ 曲线C的方程是  ……………………………………………（16分）


    同步练习册答案