题目列表(包括答案和解析)
| x2 |
| 3 |
| y2 |
| 4 |
| 15 |
| x2 |
| 3 |
| y2 |
| 4 |
| 15 |
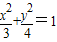的焦点，该双曲线又与直线
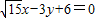交于两点A、B且OA⊥OB（O为原点）．已知曲线C：
．
（1）由曲线C上任一点E向
轴作垂线，垂足为F，动点P满足
，所成的比为
，求点P的轨迹. P的轨迹可能是圆吗？请说明理由；
（2）如果直线l的斜率为
，且过点M（0，
），直线l交曲线C于A、B两点，又
，求曲线C的方程．
已知双曲线的中心在坐标原点O上，焦点在x轴上，且浙近线方程为y＝±
，过双曲线右焦点且斜率为
的直线交双曲线于P、Q两点，又|PQ|＝4，求此双曲线方程．
一、选择题：本大题共10小题，每小题5分，共50分．
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题：本大题7小题，每小题4分，共28分．
11、
； 12、 
； 13、
； 14、
； 15、
； 16、
；17、
或
。
三、解答题
18、（1）略 …………………………………………………………………………（7分）
（2）
…………………………………………………………（14分）
19、（1）
tanA=
…………………（7分）
(2) 原式=
= 
……………………………………………………………………（14分）
20、（1）略 ……………………………………………………………………（7分）
（2）
就是二面角
的平面角，即
，
…………………………………………………………………（9分）
取
中点
，则
平面
，
就是
与平面所成的角。 …………………………（11分）
，
，
所以与平面所成的角的大小为
。 …………………………（14分）
（用向量方法，相应给分）
21、（1）
，
又
在区间（－∞，0）及（4，+∞）上都是增函数，在区间（0，4）上是减函数，
又
．………（6分）
（2）
当点
是切点时，切线方程为9x+6y－16=0．………………（10分）
当点不是切点时，切点为
，
得
所以切点为
，
切线方程为
．……………………………………（14分）
22、解：解：（1）、设
，则
，
∵点P分
所成的比为
∴ 
∴ 
∴
代入
中，得
为P点的轨迹方程．
当
时，轨迹是圆． …………………………………………………（8分）
（2）、由题设知直线l的方程为
， 设
联立方程组
，消去
得：
∵ 方程组有两解 ∴ 
且
∴
或
且
∵
∴
又 ∵
∴ 
解得
（舍去）或
∴ 曲线C的方程是
……………………………………………（16分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com