
题目列表(包括答案和解析)
如图所示,某公园要在一块绿地的中央修建两个相同的矩形的池塘,每个面积为10000米2,池塘前方要留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?

【解析】本试题主要考查了函数在实际中的运用。运用均值不等式求解函数的最值的运用。
某化工厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价。

【解析】本试题主要考查导数在研究函数中的运用。首先设变量
设宽为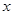 则长为
则长为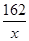 ,依题意,总造价
,依题意,总造价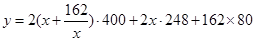
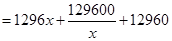
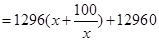
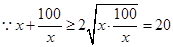 当且仅当
当且仅当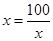 即
即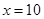 取等号
取等号
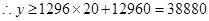 (元)得到结论。
(元)得到结论。
设宽为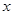 则长为
则长为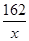 ,依题意,总造价
,依题意,总造价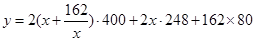
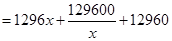
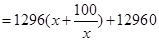
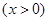 ………6分
………6分
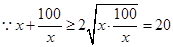 当且仅当
当且仅当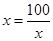 即
即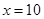 取等号
取等号
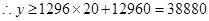 (元)……………………10分
(元)……………………10分
故当处理池宽为10米,长为16.2米时能使总造价最低,且最低总造价为38880元
某校从参加高三年级理科综合物理考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,
分,
在 记
记 分,用
分,用 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.

【解析】(1)中利用直方图中面积和为1,可以求解得到分数在 内的频率为
内的频率为
(2)中结合平均值可以得到平均分为:
(3)中用 表示抽取结束后的总记分x, 学生成绩在
表示抽取结束后的总记分x, 学生成绩在 的有
的有 人,在
人,在 的有
的有 人,在
人,在 的有
的有 人,结合古典概型的概率公式求解得到。
人,结合古典概型的概率公式求解得到。
(Ⅰ)设分数在 内的频率为
内的频率为 ,根据频率分布直方图,则有
,根据频率分布直方图,则有 ,可得
,可得 ,所以频率分布直方图如右图.……4分
,所以频率分布直方图如右图.……4分


(求解频率3分,画图1分)
(Ⅱ)平均分为: ……7分
……7分
(Ⅲ)学生成绩在 的有
的有 人,在
人,在 的有
的有 人,
人,
在 的有
的有 人.并且
人.并且 的可能取值是
的可能取值是 . ………8分
. ………8分
则 ;
; ;
;
 ;
;
 ;
; .(每个1分)
.(每个1分)
所以 的分布列为
的分布列为
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
…………………13分

如图,已知圆锥体 的侧面积为
的侧面积为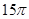 ,底面半径
,底面半径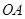 和
和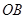 互相垂直,且
互相垂直,且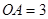 ,
, 是母线
是母线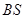 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与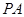 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
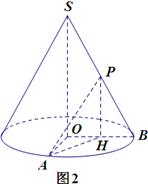
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为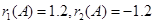 ,
, ,所以
,所以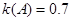
(2)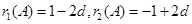 ,
,
因为 ,所以
,所以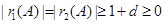 ,
,
所以
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设 ,
, ,
,
由 得定义知,
得定义知, ,
, ,
, ,
,
从而

所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使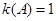 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com