如图，已知∠1 =∠2，∠B =∠C，可推得AB∥CD。理由如下：

  ∵∠1 =∠2（已   知），

且∠1 =∠CGD（__________________________）

∴∠2 =∠CGD（等量代换）                                     

∴CE∥BF（_______________________________）

∴∠       =∠BFD（__________________________）

又∵∠B =∠C（已  知）

∴∠BFD =∠B（等量代换）

∴AB∥CD（________________________________）

【解析】根据对顶角性质和已知推出∠2=∠CGD，推出CE∥BF，根据平行线的性质推出∠BFD=∠B即可

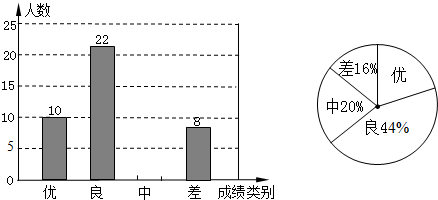
（2011•潼南县）为迎接2011年高中招生考试，某中学对全校九年级学生进行了一次数学摸底考试，并随机抽取了部分学生的测试成绩作为样本进行【解析】，绘制成了如下两幅不完整的统计图，请根据图中所给信息，【答案】下列问题：

（1）请将表示成绩类别为“中”的条形统计图补充完整；
（2）在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角是　72　度；
（3）学校九年级共有1000人参加了这次数学考试，估算该校九年级共有多少名学生的数学成绩可以达到优秀？

【答案】60°。

【考点】平行线的性质；三角形的外角性质．

【分析】利用三角形的一个外角等于与它不相邻的两个内角的和求出∠3的同位角的度数，再根据两直线平行，同位角相等即可求解．

【解答】如图，∵∠1＝130°，∠2＝70°，

∴∠4＝∠1－∠2＝130°－70°＝60°，

∵a∥b，

∴∠3＝∠4＝60°．

故答案为：60°．

【点评】本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，准确识图，理清图中各角度之间的关系是解题的关键．

完成下列证明（每空1分，共7分）

在括号内填写理由.（1） 如图，已知∠B+∠BCD=180°，∠B=∠D. 求证：∠E=∠DFE.

证明：∵∠B+∠BCD=180°(     ),

∴AB∥CD  （                                    ）

∴∠B=∠DCE（                                    ）

又∵∠B=∠D（       ）,                                                            

∴∠DCE=∠D (                                    )              

∴AD∥BE（                                       ）

∴∠E=∠DFE（                                     ）

【解析】根据平行线的判定以及平行线的性质，逐步进行分析解答即可得出答案