
题目列表(包括答案和解析)
在平面直角坐标系xOy中,以O为极点,X轴的正半轴为极轴,取与直角坐标系相同的长度单位建立极坐标系.曲线C1的参数方程为: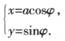 (
(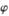 为参数);射线C2的极坐标方程为:
为参数);射线C2的极坐标方程为: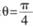 ,且射线C2与曲线C1的交点的横坐标为
,且射线C2与曲线C1的交点的横坐标为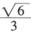
(I )求曲线C1的普通方程;
(II)设A、B为曲线C1与y轴的两个交点,M为曲线C1上不同于A、B的任意一点,若直线AM与MB分别与x轴交于P,Q两点,求证|OP|.|OQ|为定值.
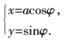 (
(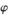 为参数);射线C2的极坐标方程为:
为参数);射线C2的极坐标方程为: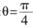 ,且射线C2与曲线C1的交点的横坐标为
,且射线C2与曲线C1的交点的横坐标为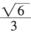
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
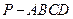
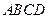
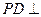
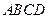
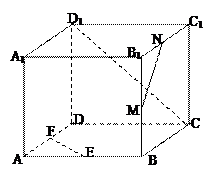
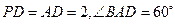 ,
, 、
、 分别为
分别为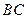 、
、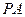 的中点。
的中点。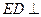 平面
平面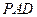 ;
;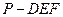 的体积;
的体积;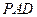 与平面
与平面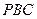 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。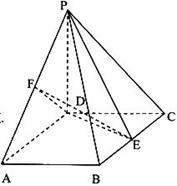
说明:
一、本解答指出了每题要考察的主要知识和能力,并给出了一种或几种解法供参考,如
果考生的解法与本解法不同,可根据试题的主要考察内容比照评分标准指定相应的评分细
则。
二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程
度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答
有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、只给整数分数,选择题和填空题不给中间分。
一、选择题:本涂考察基础知识和基本运算,每小题5分,满分50分。
1.A 2.A 3.B 4.C 5.B 6.B 7.C 8.D 9.C 10.D
二、填空题:本题考察基础知识和基本运算,每小题4分,满分20分。
11. 12.60 13.-540 14.
12.60 13.-540 14. 15.820
15.820
三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程和演算步骤。
16.本小题主要考察概率统计的基础知识,运用数学知识解决问题的能力,以及推理与运算
能力。满分13分。
(I) 、
、 同奇的取法有
同奇的取法有 种,同偶的取法有
种,同偶的取法有 ?????????????????????????????????????? 2分
?????????????????????????????????????? 2分
 ???????????????????????????????????????????????????????????????????????????????? 5分
???????????????????????????????????????????????????????????????????????????????? 5分
(Ⅱ) ,
,
 ??????????????????????? 10分
??????????????????????? 10分
其分布列为

1
2
3
4
5






 ????????????????????????????????????? 13分
????????????????????????????????????? 13分
17.本小题主要考察直线与平面的位置关系,二面角的大小,体积的计算等知识,考察空间
想象能力、逻辑思维能力和运算能力,满分13分。
 (I)连结BD,由已知得BD=2,
(I)连结BD,由已知得BD=2,
在正三角形BCD中,BE=EC,
 ,又
,又 ,
,
 …………………………2分
…………………………2分
又 平面
平面 ,
,
 ,…………………………3分
,…………………………3分
 ,
,
 平面PAD。……………………4分
平面PAD。……………………4分
(Ⅱ) ,
,
且 ,?????????????????????????????????????????????????????????????????????????????????? 5分
,?????????????????????????????????????????????????????????????????????????????????? 5分
 ??????????????????????????????????? 8分
??????????????????????????????????? 8分
 (Ⅲ)证法一:如图建立空间直角坐标系
(Ⅲ)证法一:如图建立空间直角坐标系 ,
,
则由(I)知平面 的一个法向量为
的一个法向量为
 ,
,

设平面PBC的法向量为 ,
,
由
取 得
得 ???????????????????????????????????????????????????????????????????? 11分
???????????????????????????????????????????????????????????????????? 11分
 ?????????????????????????????????????????????????? 12分
?????????????????????????????????????????????????? 12分
 平面PAD与平面PBC所成的锐二面角大小的余弦值为
平面PAD与平面PBC所成的锐二面角大小的余弦值为 ??????????????????????? 13分
??????????????????????? 13分
证法二:由(I)知 平面
平面 平面
平面 ,
,
 平面
平面 平面
平面 ???????????????????????????????????????????????????????????????????? 9分
???????????????????????????????????????????????????????????????????? 9分
又
 平面
平面 又
又 平面
平面
 平面
平面 平面
平面 ???????????????????????????????????????????????????????????????????? 10分
???????????????????????????????????????????????????????????????????? 10分
 就是平面
就是平面 与平面
与平面 所成二面角的平面角???????????????????????????? 11分
所成二面角的平面角???????????????????????????? 11分
 在
在 中,
中,
 ?????????????????????????????????????????????????????????????????? 13分
?????????????????????????????????????????????????????????????????? 13分
18.本小题主要考察两角和差公式,二倍角公式,同角三角函数关系,解斜三角形的基本知
识以及推理能力、运算能力和应用能力,满分13分。
解:在 中,
中,
 ????????????????????????????????????????????????????????????????? 2分
????????????????????????????????????????????????????????????????? 2分
化简得:
 ???????????????????????????????????????????????????????????? 4分
???????????????????????????????????????????????????????????? 4分
所以
 ????????????????????????? 6分
????????????????????????? 6分
 ???????????????????? 8分
???????????????????? 8分

即 ???????????????????????????????????????????????????????? 10分
???????????????????????????????????????????????????????? 10分
所以当 即
即 时,
时, =
= ???????????????????????????????????? 12分
???????????????????????????????????? 12分
答:当 时,所建造的三角形露天活动室的面积最大。?????????????????????????? 13分
时,所建造的三角形露天活动室的面积最大。?????????????????????????? 13分
19.本题主要考查直线、椭圆、向量等基础知识,考查曲线方程的求法以及研究曲线的定性
定量的基本方法,考查运算能力、探究能力和综合解题能力,满分13分。
解:(I)设椭圆E的方程为
由已知得:
 ???????????????????????????????????????????????????????????????????????????????? 2分
???????????????????????????????????????????????????????????????????????????????? 2分


 椭圆E的方程为
椭圆E的方程为 ??????????????????????????????????????????????????????????????? 3分
??????????????????????????????????????????????????????????????? 3分
(Ⅱ)法一:假设存在符合条件的点 ,又设
,又设 ,则:
,则:

 ????????????????????????????????????????????????? 5分
????????????????????????????????????????????????? 5分
①当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为:
的方程为: ,则
,则
由
得

 ???????????????????????????????????????????????????????? 7分
???????????????????????????????????????????????????????? 7分

所以
 ????????????????????????????????????????????? 9分
????????????????????????????????????????????? 9分
对于任意的 值,
值, 为定值,
为定值,
所以 ,得
,得 ,
,
所以 ;??????????????????????????????????????????????????????????? 11分
;??????????????????????????????????????????????????????????? 11分
②当直线 的斜率不存在时,直线
的斜率不存在时,直线
由 得
得
综上述①②知,符合条件的点 存在,起坐标为
存在,起坐标为 。????????????????????????????? 13分
。????????????????????????????? 13分
法二:假设存在符合条件的点 ,又设
,又设 则:
则:


= ????????????????????????????????????????????????? 5分
????????????????????????????????????????????????? 5分
①当直线 的斜率不为0时,设直线
的斜率不为0时,设直线 的方程为
的方程为 ,
,
由
得
 ?????????????????????????????????????????????????????????? 7分
?????????????????????????????????????????????????????????? 7分



 ????????????????????????????????????????????????? 9分
????????????????????????????????????????????????? 9分
设 则
则



 ?????????????????????????????????????????????????????????????????????????????????????? 11分
?????????????????????????????????????????????????????????????????????????????????????? 11分
②当直线 的斜率为0时,直线
的斜率为0时,直线 ,由
,由 得:
得:

综上述①②知,符合条件的点 存在,其坐标为
存在,其坐标为 ???????????????????????????????? 13分
???????????????????????????????? 13分
20.本题考查函数、导数、数列的基本知识及其应用等知识,考查化归的数学思想方法以及
推理和运算能力。考查运用数学知识分析和解决问题的能力,满分14分。
解:(I)
 ?????????????????????????????????????????? 2分
?????????????????????????????????????????? 2分
由已知得:
 ????????????????????????????????????????????????????????????????????????????????????? 4分
????????????????????????????????????????????????????????????????????????????????????? 4分
(Ⅱ)方法一:由(I)得
 在
在 上为单调增函数,则
上为单调增函数,则 恒成立,
恒成立,
即 对
对 恒成立。
恒成立。
即 对
对 恒成立,????????????????????????????????????????????????????????? 7分
恒成立,????????????????????????????????????????????????????????? 7分
令 ,
,

 ??????????????????????????????????????????????????????????????????????????????????????? 9
??????????????????????????????????????????????????????????????????????????????????????? 9
方法二:同方法一。
令
当 时
时 ,
, 在
在 单调递增,
单调递增,

 ??????????????????????????????????????????????????????????????????????????????????????? 9分
??????????????????????????????????????????????????????????????????????????????????????? 9分
(Ⅲ)方法一:

 ?????????????????????????????????????????????????????? 10分
?????????????????????????????????????????????????????? 10分
当 时,
时, ,
,
当 时,
时, ,??????????????????????????????????????????????? 12分
,??????????????????????????????????????????????? 12分
 …
…
根据题意可知 ??????????????????????????????????????? 14分
??????????????????????????????????????? 14分
方法二:同方法一,
 ???????????????????????????????????????? 10分
???????????????????????????????????????? 10分
当 时,
时,
当 时,
时, ???????????????????????????????????????????????????? 12分
???????????????????????????????????????????????????? 12分
 …
…
根据题意可知 ??????????????????????????????????????? 14分
??????????????????????????????????????? 14分
方法三:设 是数列
是数列 中的最大项,则
中的最大项,则

 ??????????????????????????? 12分
??????????????????????????? 12分
 为最大项,
为最大项,
所以 ?????????????????????????????????????????????????? 14分
?????????????????????????????????????????????????? 14分
以下同上
21.本题考查,本题满分14分
(I)本题主要考查矩阵与变换、曲线在矩阵变换下的曲线的方程,考查运算求解能力及化
归与转化思想,满分7分。
解:
 ????????????????????????????????????????????????????????????????????????????????? 2分
????????????????????????????????????????????????????????????????????????????????? 2分
 ,即
,即 ???????????????????????????????????????????????????????? 4分
???????????????????????????????????????????????????????? 4分
 ????????????????????????????????????????????????????????????????????????????????????? 5分
????????????????????????????????????????????????????????????????????????????????????? 5分

 曲线
曲线 的方程为
的方程为 ??????????????????????????????????????????????????????????? 7分
??????????????????????????????????????????????????????????? 7分
(Ⅱ)本题主要考查直线和圆的极坐标方程,考查运算求解能力及化归与转化思想,满分7
分。
解:


即 ???????????????????????????????????????????????????????????????????? 3分
???????????????????????????????????????????????????????????????????? 3分
 圆心的坐标为
圆心的坐标为 ??????????????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????????????? 4分
 ,即
,即 ???????????????????????????????????????????????????????????????? 5分
???????????????????????????????????????????????????????????????? 5分

 圆心到直线的距离为1?????????????????????????????????????????????????????????????????????? 7分
圆心到直线的距离为1?????????????????????????????????????????????????????????????????????? 7分
(Ⅲ)本题主要考查利用常见不等式求条件最值,考查化归与转化思想,满分7分
解:
 ????????????????????????????????????????? 3分
????????????????????????????????????????? 3分
 ?????????????????????????????????????????????????????????????????? 5分
?????????????????????????????????????????????????????????????????? 5分
当且仅当 即
即 时取到“=”号,
时取到“=”号,
 当
当 时
时 的最小值为
的最小值为 ??????????????????????????????? 7分
??????????????????????????????? 7分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com