
题目列表(包括答案和解析)
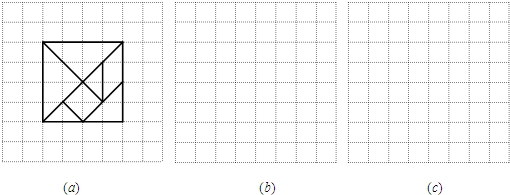

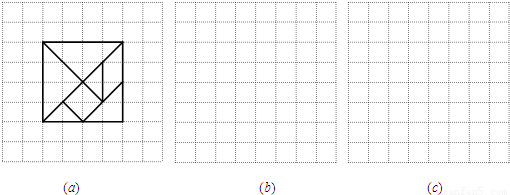
 .你同意他的说法吗?说说你的理由.
.你同意他的说法吗?说说你的理由.
选择题: CABDA BBADA BB
4、原式卷.files/image270.gif)
由条件可求得:卷.files/image272.gif)
卷.files/image274.gif) 原式
原式卷.files/image276.gif) 故选D
故选D
5、由题得卷.files/image278.gif) ,则
,则卷.files/image280.gif) 是公比为
是公比为卷.files/image140.gif) 的等比数列,则
的等比数列,则卷.files/image283.gif) ,故选答案
,故选答案卷.files/image159.gif)
卷.files/image285.jpg) 6、由已知可得
6、由已知可得卷.files/image287.gif) ,直线
,直线卷.files/image289.gif) 的方程
的方程卷.files/image291.gif) ,
,
卷.files/image274.gif) 直线
直线卷.files/image289.gif) 过两个整点
过两个整点卷.files/image295.gif) ,(
,(卷.files/image297.gif) ),即
),即卷.files/image299.gif) ,故应选B
,故应选B
7、令卷.files/image301.gif) ,则
,则卷.files/image303.gif) ,其值域为
,其值域为卷.files/image305.gif) .由
.由
对数函数的单调性可知:卷.files/image307.gif) ,且
,且卷.files/image309.gif) 的最小值
的最小值卷.files/image311.gif) 而
而卷.files/image307.gif) ,
,
故选答案卷.files/image161.gif) 。
。
8、共有卷.files/image315.gif) 个四位数,其中个位数字是1,且恰好有两个相同数字的四位数分为两类:一类:“
个四位数,其中个位数字是1,且恰好有两个相同数字的四位数分为两类:一类:“卷.files/image317.gif) 个;另一类;其他三个数字之一重复,有
个;另一类;其他三个数字之一重复,有卷.files/image319.gif) 种。所以答案为:A
种。所以答案为:A
9、由题意可知满足卷.files/image321.gif) 的
的卷.files/image323.gif) 的轨迹是双曲线的右支,根据“单曲线型直线”的定义可知,就是求哪条直线与双曲线的右支有交点,故选D
的轨迹是双曲线的右支,根据“单曲线型直线”的定义可知,就是求哪条直线与双曲线的右支有交点,故选D
10、选卷.files/image159.gif) 。可以证明D点和AB的中点E到P点和C点的距离相等,所以排除B和C选项。满足
。可以证明D点和AB的中点E到P点和C点的距离相等,所以排除B和C选项。满足卷.files/image114.gif) 的点在PC的中垂面上,PC的中垂面与ABCD的交线是直线,从而选A。
的点在PC的中垂面上,PC的中垂面与ABCD的交线是直线,从而选A。
11、解:以卷.files/image327.gif) 的平分线所在直线为
的平分线所在直线为卷.files/image329.gif) 轴,建立坐标系,设
轴,建立坐标系,设卷.files/image331.gif) ,则
,则卷.files/image333.gif) 则
则卷.files/image335.gif) 、
、卷.files/image337.gif) 、
、卷.files/image339.gif) ,
,
所以
卷.files/image341.gif)
卷.files/image343.gif) ,故当且仅当
,故当且仅当卷.files/image345.gif) ,即
,即卷.files/image347.gif) 为正三角形时,
为正三角形时,卷.files/image349.gif) 故选B
故选B
12、卷.files/image351.gif) 则
则卷.files/image353.gif) ,
,
卷.files/image355.gif) ,
,卷.files/image357.gif)
卷.files/image359.gif)
故卷.files/image361.gif) 则
则卷.files/image363.gif) 的最小值为
的最小值为卷.files/image140.gif) ,故选答案
,故选答案卷.files/image161.gif) 。
。
二、填空题
13、卷.files/image367.gif) 。
。
14、利用正弦定理可将已知等式变为卷.files/image369.gif) 即
即卷.files/image371.gif) ,
,
卷.files/image373.gif) ,
, 卷.files/image375.gif)
卷.files/image377.gif)
卷.files/image379.gif)
卷.files/image380.jpg)
卷.files/image274.gif) 当
当卷.files/image383.gif) 时,
时,卷.files/image385.gif) 有最大值
有最大值卷.files/image387.gif)
15、卷.files/image389.gif) 。
。
16、卷.files/image391.gif) 。画图分析得
。画图分析得卷.files/image393.gif) 球
球卷.files/image057.gif) 在二面角
在二面角卷.files/image169.gif) 内的那一部分的体积是球的体积的
内的那一部分的体积是球的体积的卷.files/image140.gif) ,所以
,所以卷.files/image398.gif) 。
。
三、解答题:
17、解:卷.files/image400.gif)
卷.files/image402.gif)
(1)由卷.files/image404.gif) 得
得卷.files/image406.gif) 或
或卷.files/image408.gif)
卷.files/image410.gif) 在
在卷.files/image412.gif) 上是增函数,
上是增函数,卷.files/image414.gif)
可额卷.files/image416.gif) 可得
可得卷.files/image418.gif)
卷.files/image420.jpg) 18、(1)如图建立空间直角坐标系,则
18、(1)如图建立空间直角坐标系,则卷.files/image422.gif)
卷.files/image424.gif)
设卷.files/image426.gif)
卷.files/image428.gif) 分别为
分别为卷.files/image430.gif) 的重心,
的重心,卷.files/image432.gif) ,
,
卷.files/image434.gif)
卷.files/image436.gif) ,即
,即卷.files/image200.gif)
(2)(i)卷.files/image439.gif) 平面
平面卷.files/image441.gif) ,
,卷.files/image443.gif)
卷.files/image445.gif)
卷.files/image447.gif) ,平面
,平面卷.files/image441.gif) 的法向量为
的法向量为卷.files/image450.gif) ,
,
平面卷.files/image452.gif) 的法向量为
的法向量为卷.files/image454.gif)
故卷.files/image456.gif) ,即二面角
,即二面角卷.files/image206.gif) 的大小为
的大小为卷.files/image459.gif)
(ii)设平面卷.files/image461.gif) 的法向量
的法向量卷.files/image463.gif) ,
,
卷.files/image465.gif) ,由
,由卷.files/image467.gif) 解得
解得卷.files/image469.gif)
又卷.files/image471.gif) ,
,卷.files/image274.gif) 点
点卷.files/image208.gif) 到平面
到平面卷.files/image475.gif) 的距离为
的距离为卷.files/image477.gif)
18、解:(I)抽取的球的标号卷.files/image329.gif) 可能为1,2,3,4
可能为1,2,3,4
卷.files/image153.jpg) 则
则卷.files/image480.gif) 分别为0,1,2,3:
分别为0,1,2,3:卷.files/image482.gif) 分别为
分别为卷.files/image484.gif)
因此卷.files/image216.gif) 的所有取值为0,1,2,3,4,5
的所有取值为0,1,2,3,4,5
当卷.files/image487.gif) 时,
时,卷.files/image216.gif) 可取最大值5,此时
可取最大值5,此时卷.files/image490.gif)
(Ⅱ)当卷.files/image492.gif) 时,
时,卷.files/image494.gif) 的所有取值为(1,2),此时
的所有取值为(1,2),此时卷.files/image496.gif) ;
;
当卷.files/image498.gif) 时,
时,卷.files/image494.gif) 的所有取值为(1,1),(1,3),(2,2),此时
的所有取值为(1,1),(1,3),(2,2),此时卷.files/image501.gif)
当卷.files/image503.gif) 时,
时,卷.files/image494.gif) 的所有取值为(1,4),(2,1),(2,3),(3,2)此时
的所有取值为(1,4),(2,1),(2,3),(3,2)此时卷.files/image505.gif)
当卷.files/image507.gif) 时,
时,卷.files/image494.gif) 的所有取值为(2,4),(3,1),(3,3),(4,2)此时
的所有取值为(2,4),(3,1),(3,3),(4,2)此时卷.files/image509.gif)
当卷.files/image511.gif) 时,
时,卷.files/image494.gif) 的所有取值为(3,4),(4,1),(4,3),此时
的所有取值为(3,4),(4,1),(4,3),此时卷.files/image513.gif)
故卷.files/image216.gif) 的分布列为:
的分布列为:
卷.files/image216.gif)
0
1
2
3
4
5
卷.files/image323.gif)
卷.files/image518.gif)
卷.files/image520.gif)
卷.files/image522.gif)
卷.files/image522.gif)
卷.files/image520.gif)
卷.files/image518.gif)
卷.files/image527.gif) 。
。
20解:(1)卷.files/image529.gif)
卷.files/image531.gif) 故
故卷.files/image533.gif) 。
。
(Ⅱ)由(I)知卷.files/image535.gif)
令卷.files/image537.gif) 则
则卷.files/image539.gif) 。当
。当卷.files/image541.gif) 时,
时,卷.files/image543.gif) ;
;
当卷.files/image545.gif) 时,
时,卷.files/image547.gif)
卷.files/image549.gif)
卷.files/image551.gif)
(Ⅲ)卷.files/image553.gif) ,
,
卷.files/image555.gif)
①-②得
卷.files/image557.gif)
令卷.files/image559.gif) 则
则卷.files/image561.gif)
卷.files/image563.gif) 。
。
卷.files/image565.gif) 则
则卷.files/image567.gif) 。
。
卷.files/image569.gif) 而
而卷.files/image571.gif)
卷.files/image573.gif) 。
。
卷.files/image574.jpg)
卷.files/image575.jpg) 21、(I)解:依题设得椭圆的方程为
21、(I)解:依题设得椭圆的方程为卷.files/image577.gif) ,
,
直线卷.files/image579.gif) 的方程分别为
的方程分别为卷.files/image581.gif)
如图,设卷.files/image583.gif) 其中
其中卷.files/image585.gif) ,
,
且卷.files/image212.gif) 满足方程
满足方程卷.files/image588.gif) 故
故卷.files/image590.gif) ①
①
由卷.files/image248.gif) 知
知卷.files/image593.gif) 得
得卷.files/image595.gif)
由卷.files/image244.gif) 在
在卷.files/image242.gif) 上知
上知卷.files/image599.gif) 得
得卷.files/image601.gif) 。
。
所以卷.files/image603.gif) ,化简得
,化简得卷.files/image605.gif) ,
,
解得卷.files/image607.gif) 或
或卷.files/image609.gif) 。
。
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点卷.files/image611.gif) ,
,卷.files/image613.gif) 到
到卷.files/image242.gif) 的距离分别为
的距离分别为
卷.files/image616.gif) ,
,
卷.files/image618.gif)
又卷.files/image620.gif) ,所以四边形
,所以四边形卷.files/image252.gif) 的面积为
的面积为
卷.files/image623.gif) ,
,
当卷.files/image625.gif) 即当
即当卷.files/image627.gif) 时,上式取等号,所以
时,上式取等号,所以卷.files/image629.gif) 的最大值为2
的最大值为2卷.files/image142.gif) 。
。
解法二:由题设,卷.files/image632.gif) ,
,
设卷.files/image634.gif) 由①得
由①得卷.files/image636.gif) ,
,
故四边形卷.files/image252.gif) 的面积为
的面积为卷.files/image639.gif) +
+卷.files/image641.gif) =
=卷.files/image643.gif)
卷.files/image645.gif)
当卷.files/image647.gif) 时,上式取等号,所以
时,上式取等号,所以卷.files/image629.gif) 的最大值为
的最大值为卷.files/image650.gif)
22、解:(I)由题设可得卷.files/image652.gif)
卷.files/image654.gif) 函数
函数卷.files/image309.gif) 在
在卷.files/image657.gif) 上是增函数,
上是增函数,
卷.files/image274.gif) 当
当卷.files/image660.gif) 时,不等式
时,不等式卷.files/image662.gif) 即
即卷.files/image664.gif) 恒成立。
恒成立。
卷.files/image654.gif) 当
当卷.files/image660.gif) 时,
时,卷.files/image668.gif) 的最大值为1,则实数
的最大值为1,则实数卷.files/image016.gif) 的取值范围是
的取值范围是卷.files/image657.gif) ;
;
(Ⅱ)当卷.files/image261.gif) 时,
时,卷.files/image673.gif)
卷.files/image274.gif) 当
当卷.files/image676.gif) 时,
时,卷.files/image678.gif) ,于是
,于是卷.files/image309.gif) 在
在卷.files/image681.gif) 上单调递减;
上单调递减;
卷.files/image682.jpg) 当
当卷.files/image684.gif) 时,
时,卷.files/image686.gif) ,于是
,于是卷.files/image309.gif) 在
在卷.files/image689.gif) 上单调递增。
上单调递增。
又卷.files/image691.gif)
综上所述,当卷.files/image693.gif) 时,函数
时,函数卷.files/image309.gif) 在
在卷.files/image264.gif) 上的最小值为
上的最小值为卷.files/image697.gif) ,当
,当卷.files/image699.gif) 时,
时,
函数卷.files/image309.gif) 在
在卷.files/image264.gif) 上的最大值为
上的最大值为卷.files/image703.gif)
(Ⅲ)当卷.files/image261.gif) 时,由(Ⅰ)知
时,由(Ⅰ)知卷.files/image706.gif) 在
在卷.files/image657.gif) 上是增函数
上是增函数
卷.files/image274.gif) 对于任意的正整数
对于任意的正整数卷.files/image710.gif) ,有
,有卷.files/image712.gif) ,则
,则卷.files/image714.gif)
即卷.files/image716.gif) ,
,卷.files/image718.gif) 。
。
卷.files/image720.gif) 。
。
而卷.files/image722.gif) 则
则卷.files/image724.gif) 成立,
成立,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com