题目列表(包括答案和解析)
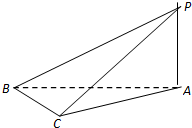如图，在三棱锥P-ABC中，∠PAB=∠PAC=∠ACB=90°．
如图，四棱锥P-ABCD中，PA⊥底面ABCD，
，BC=CD=2，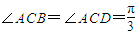
．如图所示，PA⊥平面ABCD，底面ABCD为菱形，
为PC的中点．
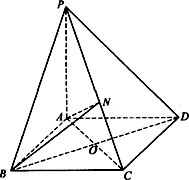
(1)求证：BD⊥平面PAC；
(2)求证：PA∥平面NBD；
(3)求二面角B－AN－C的平面角的大小．
如图，四棱锥P－ABCD中，PA⊥底面ABCD，
，BC＝CD＝2，
．
(Ⅰ)求证：BD⊥平面PAC；
(Ⅱ)若侧棱PC上的点F满足PF＝7FC，求三棱锥P－BDF的体积．
如图,在四棱锥P-ABCD中，底面ABCD是正方形，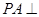
底面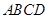
,且PA=AB.
（1）求证：BD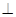
平面PAC；
（2）求异面直线BC与PD所成的角.
一、选择题（本大题共12个小题，每小题5分，共60分）
1―5 CABDC 6―10 DCCBB 11―12AB
二、填空题：
13．9
14．
15．（1，0）
16．420
三、解答题：
17．解：（1）
（2）由（1）知，
18．解： 记“第i个人过关”为事件Ai（i=1，2，3），依题意有
。
（1）设“恰好二人过关”为事件B，则有
，
且
彼此互斥。
于是
=
（2）设“有人过关”事件G，“无人过关”事件
互相独立，
19．解法：1：（1）
（2）过E作EF⊥PC，垂足为F，连结DF。 （8分）
|
解得
（6分）
，列表如下：
因为直线l与椭圆交点在y轴右侧，
解得2
。
（4分）
得
（λ≠0）。 （9分）
解得
（14分）
