
题目列表(包括答案和解析)



 的通项公式;
的通项公式; ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由数列![]() 的通项公式
的通项公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述结果推测出计算f(n)的公式,并用数学归纳法加以证明.
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。
成立的所有n中的最小值。
(1)若![]() ,求b3;
,求b3;
(2)若![]() ,求数列
,求数列![]() 的前2m项和公式;
的前2m项和公式;
(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列 的通项公式为
的通项公式为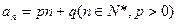 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
一、选择题(本大题共12个小题,每小题5分,共60分)
1―5 CABDC 6―10 DCCBB 11―12AB
二、填空题:
13.9
14.
15.(1,0)
16.420
三、解答题:
17.解:(1)

(2)由(1)知,

18.解: 记“第i个人过关”为事件Ai(i=1,2,3),依题意有
 。
。
(1)设“恰好二人过关”为事件B,则有 ,
,
且 彼此互斥。
彼此互斥。
于是
=
(2)设“有人过关”事件G,“无人过关”事件 互相独立,
互相独立,

19.解法:1:(1)

(2)过E作EF⊥PC,垂足为F,连结DF。 (8分)
|