
题目列表(包括答案和解析)
3+
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
如图,三棱锥 中,侧面
中,侧面 底面
底面 ,
,  ,且
,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面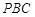 ;
;
(Ⅱ)若 为侧棱PB的中点,求直线AE与底面
为侧棱PB的中点,求直线AE与底面 所成角的正弦值.
所成角的正弦值.

【解析】第一问中,利用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以 第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证
第二问中结合取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,又EH//PO,所以EH平面
平面ABC,又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,

解
(Ⅰ) 证明:由用由 知,
知,  ,
,
又AP=PC=2,所以AC=2 ,
,
又AB=4, BC=2 ,,所以
,,所以 ,所以
,所以 ,即
,即 ,
,
又平面 平面ABC,平面
平面ABC,平面 平面ABC=AC,
平面ABC=AC,  平面ABC,
平面ABC,
 平面ACP,所以
平面ACP,所以
………………………………………………6分
(Ⅱ)如图, 取AC中点O,连接PO、OB,并取OB中点H,连接AH、EH,
因为PA=PC,所以PO⊥AC,同(Ⅰ)易证 平面ABC,
平面ABC,
又EH//PO,所以EH平面 ABC ,
ABC ,
则 为直线AE与底面ABC 所成角,
为直线AE与底面ABC 所成角,
且 ………………………………………10分
………………………………………10分
又PO=1/2AC= ,也所以有EH=1/2PO=
,也所以有EH=1/2PO= ,
,
由(Ⅰ)已证 平面PBC,所以
平面PBC,所以 ,即
,即 ,
,
故 ,
,
于是
所以直线AE与底面ABC 所成角的正弦值为

如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形, ,
, ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)设PD=AD=a, 求三棱锥B-EFC的体积.

【解析】第一问利用线面平行的判定定理, ,得到
,得到
第二问中,利用
 ,所以
,所以
又因为 ,
, ,从而得
,从而得
第三问中,借助于等体积法来求解三棱锥B-EFC的体积.
(Ⅰ)证明:
 分别是
分别是 的中点,
的中点, 
 ,
, . …4分
. …4分
(Ⅱ)证明: 四边形
四边形 为正方形,
为正方形, .
.
 ,
,  .
.
 ,
,  ,
,
 .
. ,
, . ………8分
. ………8分
(Ⅲ)解:连接AC,DB相交于O,连接OF, 则OF⊥面ABCD,
∴

已知函数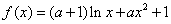 .
.
(Ⅰ)讨论函数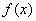 的单调性;
的单调性;
(Ⅱ)设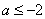 ,证明:对任意
,证明:对任意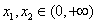 ,
,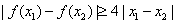 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
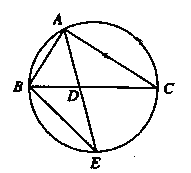
如图, 的角平分线
的角平分线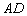 的延长线交它的外接圆于点
的延长线交它的外接圆于点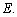
(Ⅰ)证明: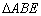 ∽△
∽△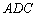 ;
;
(Ⅱ)若 的面积
的面积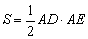 ,求
,求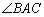 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com