
题目列表(包括答案和解析)
已知向量:![]() ,
,
函数![]() ,若
,若![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]()
(1)求![]() 的值,并求
的值,并求![]() 的最大值及相应x的集合;
的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△ABC的面积![]() ,求边a的长.
,求边a的长.
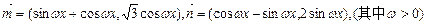 ,
,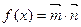 ,若
,若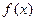 相邻两对称轴间的距离为
相邻两对称轴间的距离为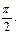
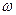 的值,并求
的值,并求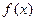 的最大值及相应x的集合;
的最大值及相应x的集合;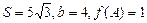 ,求边a的长.
,求边a的长.| m |
| 3 |
| n |
| m |
| n |
| π |
| 2 |
| 3 |
. |
| a |
. |
| b |
| 3 |
. |
| a |
. |
| b |
| π |
| 3 |
| π |
| 6 |
| m |
| m |
| m |
| a |
| b |
| c |
| 5 |
| a |
| b |
| c |
| 5 |
| 2 |
| a |
| c |
一、选择题:本大题共12小题,每小题5分,共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
B
A
C
A
C
D
D
B
C
二、填空题:本大题共4小题,每小题4分,共16分.
13. 14.
14. 15.
15. 16.(-1,0)
16.(-1,0)
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.解:(1)
 ………………3分
………………3分
又题意可得 ………………4分
………………4分
当 =1时,
=1时, 有最大值为2,
有最大值为2,
 ………………6分
………………6分
(2) ……7分
……7分
 …………………8分
…………………8分
 …………………9分
…………………9分
由余弦定理得:a2=16+25-2×4×5cos =21
=21  …………12分
…………12分
18.解:(1) 抽取的全部结果所构成的基本事件空间为:
Ω={(-2,-2),(-2,3),(-1,-2),(-1,3),(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3)}
共10个基本事件 ………………2分
设使函数为增函数的事件空间为A:
则A={(1,-2),(1,3),(2,-2),(2,3),(3,-2),(3,3)}有6个基本事件 ………………4分
所以,  …………………6分
…………………6分
(2) m、n满足条件m+n-1≤0 -1≤m≤1 -1≤n≤1的区域如图所示:
使函数图像过一、二、三象限的(m,n)为区域为第一象限的阴影部分
 ∴所求事件的概率为
∴所求事件的概率为 ………………12分
………………12分
19.解:(1).连 ,四边形
,四边形 菱形
菱形
 ,
,




 ……………2分
……………2分


 为
为 的中点,
的中点,

又
 ,……………4分
,……………4分

 ………6分
………6分
(2).当 时,使得
时,使得 …………7分
…………7分
连 交
交 于
于 ,交
,交 于
于 ,则
,则 为
为 的中点,
的中点,
又
 为
为 边
边 上中线,
上中线,
 为正三角形
为正三角形 的中心,令菱形
的中心,令菱形 的边长为
的边长为 ,则
,则 ,
, 。
。



 ……………………10分
……………………10分
 即:
即:
 。 ………………12分
。 ………………12分
20.解:(1)
 是等差数列, …………………1分
是等差数列, …………………1分

 从第二项开始是等比数列,
从第二项开始是等比数列,  ………………6分
………………6分
(2) ………………7分
………………7分

 ………………10分
………………10分
错位相减并整理得 ………………12分
………………12分
21.解:(1)∵点A在圆 ,
,
 …………3分
…………3分
由椭圆的定义知:|AF1|+|AF2|=2a,
 ……………5分
……………5分
(2)∵函数
点F1(-1,0),F2(1,0), ………………6分
①若 ,
,
 ……………7分
……………7分
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由 …(*)
…(*)
 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根
 ………………9分
………………9分


 ……10分
……10分

由①②知 ………………12分
………………12分
22.解:(1)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同
 …………………2分
…………………2分
由题意知 ,∴
,∴ ……4分
……4分
由 得,
得, ,或
,或 (舍去)
(舍去)
即有 …………………6分
…………………6分
(2)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同

由题意知 ,∴
,∴
由 得,
得, ,或
,或 (舍去) ………………9分
(舍去) ………………9分
即有 ……………10分
……………10分
令 ,则
,则 ,于是
,于是
当 ,即
,即 时,
时, ;
;
当 ,即
,即 时,
时, …………………13分
…………………13分
故 在
在 的最大值为
的最大值为 ,故
,故 的最大值为
的最大值为 ………………14分
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com