20090323
13．9
14．
15．（1，0）
16．420
三、解答题：
17．解：（1）
（2）由（1）知，
18．解：设“通过第一关”为事件A1，“补过且通过第一关”为事件A2，“通过第二关”为事件B1，“补过且通过第二关”为事件B2。
（2分）
（1）不需要补过就可获得奖品的事件为A=A1?B1，又A1与B1相互独立，则P（A）=P
（A1?B1）=P（A1）?P（B1）=
。故他不需要补过就可获得奖品的概率为
。
（6分）
（2）由已知得ξ=2，3，4，注意到各事件之间的独立性与互斥性，可得
19．解法：1：（1）
（2）过E作EF⊥PC，垂足为F，连结DF。
（8分）
由Rt△EFC∽ 
解法2：（1） 
（2）设平面PCD的法向量为 则  解得  AC的法向量取为 
角A―PC―D的大小为 20．（1）由已知得  是以a2为首项，以  （6分） （2）证明：  21：解（1）由线方程x+2y+10-6ln2=0知， 直线斜率为  所以
解得a=4，b=3。 （6分） （2）由（1）得 令 
22．解：（1）设直线l的方程为 得 因为直线l与椭圆交点在y轴右侧， 所以 解得2 故l直线y截距的取值范围为 。
（4分） （2）①（Ⅰ）当AB所在的直线斜率存在且不为零时， 设AB所在直线方程为 解方程组
得 所以 设 所以 因为l′是AB的垂直平分线，所以直线l′的方程为 因此 又 （Ⅱ）当k=0或不存在时，上式仍然成立。 综上所述，M的轨迹方程为 （λ≠0）。 （9分） ②当k存在且k≠0时，由（1）得 由 解得 所以 
解法：（1）由于 
当且仅当4+5k2=5+4k2，即k≠±1时等号成立， 此时， 当 当k不存在时， 综上所述，
（14分） 解法（2）： 因为 又 当且仅当4+5k2=5+4k2，即k≠±1时等号成立， 此时。 当 当k不存在时， 综上所述，。
| | | |
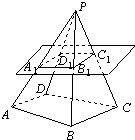设四棱锥P-ABCD的底面不是平行四边形，用平面 α去截此四棱锥，使得截面四边形是平行四边形，则这样的平面α（ ）
的底面不是平行四边形，用平面
去截此四棱锥，使得截面是平行四边形，则这样的平面