
题目列表(包括答案和解析)
己知函数f(x)=![]() ,A
,A![]() R.
R.
(1)证明:函数y=f(x)的图象关于点(A,-1)成中心对称图形;
(2)当 x![]() [A+1,A+2]时,求证:f(x)
[A+1,A+2]时,求证:f(x)
![]() [-2,-
[-2,-![]() ];
];
(3)我们利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),….
在上述构造数列的过程中,如果xi+(I=2,,3,4,…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个常数列{xn},求实数A的取值范围;
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{ xn},求实数A的值.
(1)证明:函数y=f(x)的图象关于点(A,-1)成中心对称图形;
(2)当 x![]() [A+1,A+2]时,求证:f(x)
[A+1,A+2]时,求证:f(x)
![]() [-2,-
[-2,-![]() ];
];
(3)我们利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),….
在上述构造数列的过程中,如果xi+(I=2,,3,4,…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个常数列{xn},求实数A的取值范围;
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{ xn},求实数A的值.
已知函数f(x)的定义域为[-1,5],部分对应值如下表.
f(x)的导函数y=![]() (x)的图象如图所示:
(x)的图象如图所示:
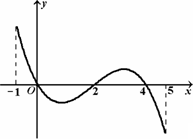
下列关于f(x)的命题:
①函数f(x)是周期函数;
②函数f(x)在[0,2]是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点;
⑤函数y=f(x)-a的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是________.
已知向量p=(a,x+1),q=(x,a),m=(1,y),且(p-q)∥m,y与x的函数关系式为y=f(x).
(1)求f(x);
(2)判断并证明函数y=f(x)当x>a时的单调性;
(3)我们利用函数y=f(x)构造一个数列{xn),方法如下:对于f(x)定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),….在上述构造数列的过程中,如果xi(i=1,2,3,4,…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.如果取f(x)定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的值.
已知f(x)是以2为周期的偶函数,当x∈[0, 1]时,f(x)=x,那么在区间[-1,3]内关于x的方程f(x)=kx+k+1(k∈R,k≠-1)的根的个数
A.不可能有3个 B.最少有1个,最多有4个
C.最少有1个,最多有3个 D.最少有2个,最多有4个
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com