
题目列表(包括答案和解析)
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C=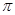 , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: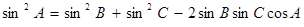
(2) 若锐角A, B, C满足A+B+C=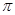 , 则
, 则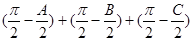 =
=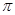 , 以
, 以
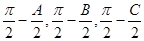 分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: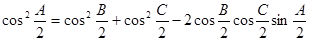 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C=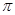 , 类比上面推理方法, 可以得到一个等式是 .
, 类比上面推理方法, 可以得到一个等式是 .
在△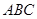 中,
中,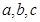 分别为内角
分别为内角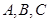 的对边,且
的对边,且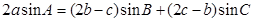 .
.
(1)求角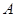 的大小;
的大小;
(2)若 +
+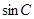 =
=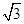 ,试判断△
,试判断△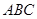 的形状.
的形状.
【解析】本试题主要考查了解三角形中正弦定理和余弦定理的运用。求解变和角,并定形的问题。
观察下面两个推理过程及结论:
(1)若锐角A,B,C满足A+B+C=![]() ,以角A,B,C分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:
,以角A,B,C分别为内角构造一个三角形,依据正弦定理和余弦定理可得到等式:![]()
(2) 若锐角A,B,C满足A+B+C=![]() ,则
,则![]() ,以角
,以角![]() 分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式
分别为内角构造一个三角形,依据正弦定理和余弦定理可以得到的等式![]() .则若锐角A,B,C满足A+B+C=
.则若锐角A,B,C满足A+B+C=![]() ,类比上面推理方法,可以得到一个等式是 .
,类比上面推理方法,可以得到一个等式是 .
已知 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
【解析】本试题主要是考查了解三角形中正弦定理和正弦面积公式的求解运用。
(1)因为 ,利用正弦定理得到C的值。
,利用正弦定理得到C的值。
(2)根据 ,然后结合余弦定理得到C的值。
,然后结合余弦定理得到C的值。
已知向量 =(
=( ),
), =(
=(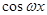 ,
,
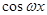 ),其中(
),其中(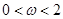 ).函数
).函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若 =1,b=l,S△ABC=
=1,b=l,S△ABC= ,求a的值.
,求a的值.
【解析】第一问利用向量的数量积公式表示出
 ,然后利用
,然后利用 得到
得到 ,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
,从而得打解析式。第二问中,利用第一问的结论,表示出A,结合正弦面积公式和余弦定理求解a的值。
解:因为

由余弦定理得 ,……11分故
,……11分故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com