
题目列表(包括答案和解析)
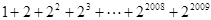 的值,
的值,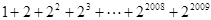 ,
,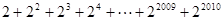 ,因此2S-S=
,因此2S-S=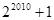 ,
,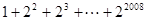 =
=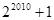 仿照以上推理计算
仿照以上推理计算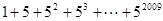 的值是( )
的值是( )A.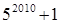 | B.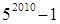 | C.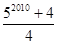 | D.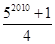 |
在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:  ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ 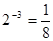 ,∴
,∴  .
.
1.根据定义计算:(本小题6分)
① =____;②
=____;② =
;
=
;
③如果 ,那么x= 。
,那么x= 。
2.设 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵ ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出:
 =
.(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
=
.(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
3.请你猜想: (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
在形如![]() 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果![]() (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ![]() ,例如:求
,例如:求 ,因为
,因为 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ![]() ,∴
,∴ ![]() .
.
1.根据定义计算:(本小题6分)
① =____;②
=____;② = ;
= ;
③如果![]() ,那么x= 。
,那么x= 。
2.设 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵![]() ,∴
,∴![]() ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出:
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
3.请你猜想: (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算; (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求 ,因为
,因为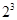 =8,所以
=8,所以 =3;又比如∵
=3;又比如∵ ,∴
,∴ .
. =____;②
=____;② = ;
= ; ,那么x= 。
,那么x= 。 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数), ,∴
,∴ ∴
∴ ,
,
 = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分) (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com