
题目列表(包括答案和解析)
(本小题满分12分)
已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且
上,且
满足![]() .
.
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]() 、
、![]() 为轨迹
为轨迹![]() 上两点,且
上两点,且![]() >1,
>1, ![]() >0,
>0,![]() ,求实数
,求实数![]() ,
,
使![]() ,且
,且![]() .
.
(本小题满分12分)
已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且
上,且
满足![]() . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]() 、
、![]() 为轨迹
为轨迹![]() 上两点,且
上两点,且![]() >1,
>1, ![]() >0,
>0,![]() ,求实数
,求实数![]() ,
,
已知点 ,点
,点 在
在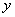 轴上,点
轴上,点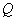 在
在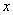 轴的正半轴上,点
轴的正半轴上,点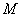 在直线
在直线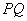 上,且
上,且
满足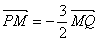 ,
,
(Ⅰ)当点 在
在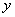 轴上移动时,求点
轴上移动时,求点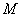 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设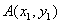 、
、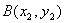 为轨迹
为轨迹 上两点,且
上两点,且 >1,
>1,
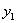 >0,
>0,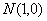 ,若
,若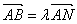 且
且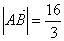 ,求实数
,求实数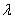 .
.
(本小题满分12分)
已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上 ,且满足
上 ,且满足![]() ,
,![]() .
.
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]()
![]() 为轨迹
为轨迹![]() 上两点,且
上两点,且![]() ,
,![]() ,求实数
,求实数![]() ,使
,使![]() ,且
,且![]() .
.
已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)设![]() ,
,![]() 为抛物线上两点,且
为抛物线上两点,且![]() 不与
不与![]() 轴垂直,若线段
轴垂直,若线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() ,求证:线段
,求证:线段![]() 中点的横坐标为定值.
中点的横坐标为定值.
评分说明:
1. 第一题选择题,选对得分,不选、错选或多选一律得0分.
2. 第二题填空题,不给中间分.
3. 解答与证明题,本答案给出了一种或几种解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制定相应的评分细则.
4. 对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
5. 解答右侧所注分数,表示考生正确做到这一步应得的累加分数.
6. 只给整数分数.
一、选择题
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
答案
C
B
B
D
A
A
C
B
A
C
D
B
二、填空题
题号
(13)
(14)
(15)
(16)
答案
.files/image343.gif)
25
.files/image345.gif)
-30
三、解答题
(17)解:(Ⅰ)∵.files/image054.gif) //
//.files/image018.gif) ∴
∴.files/image349.gif) ………………………1分
………………………1分
∴.files/image351.gif) . 即
. 即.files/image353.gif) . …………………………3分
. …………………………3分
又∵.files/image004.gif) 为锐角,∴
为锐角,∴.files/image356.gif) . …………………………………………4分
. …………………………………………4分
∴.files/image358.gif) ,∴
,∴.files/image360.gif) . …………………………………………………5分
. …………………………………………………5分
(Ⅱ)由余弦定理.files/image362.gif) 有
有.files/image364.gif) ,解得
,解得.files/image366.gif) 或
或
.files/image368.gif) . ………………………………………………………………………8分
. ………………………………………………………………………8分
当.files/image368.gif) 时,
时,.files/image371.gif) ;当
;当.files/image366.gif) 时,
时,.files/image373.gif)
……………………………………10分
(18)解:(Ⅰ)∵随意抽取4件产品检查是随机事件,而第一天有9件正品.
∴第一天通过检查的概率为.files/image375.gif) . ……………………………5分
. ……………………………5分
(Ⅱ)同(Ⅰ),第二天通过检查的概率为.files/image377.gif) . …………………9分
. …………………9分
因第一、第二天是否通过检查相互独立, ……………………………10分
所以,两天全部通过检查的概率为.files/image379.gif) . …………12分
. …………12分
.files/image380.jpg) (19)解:(Ⅰ)∵
(19)解:(Ⅰ)∵.files/image382.gif) 为常数,∴
为常数,∴.files/image384.gif) . ………………2分
. ………………2分
∴.files/image386.gif) .
.
又.files/image388.gif) 成等比数列,∴
成等比数列,∴.files/image390.gif) ,解得
,解得.files/image392.gif) 或
或.files/image394.gif) .…4分
.…4分
当.files/image392.gif) 时,
时,.files/image396.gif) 不合题意,舍去. ∴
不合题意,舍去. ∴.files/image394.gif) . …………………6分
. …………………6分
(Ⅱ)由(Ⅰ)知,.files/image398.gif) . ………………………………………………8分
. ………………………………………………8分
∴.files/image400.gif) …………10分
…………10分
∴.files/image402.gif)
.files/image404.gif) …………………………………………12分
…………………………………………12分
(20)解法一:
(Ⅰ)取.files/image406.gif) 的中点
的中点.files/image408.gif) ,连
,连.files/image410.gif) ,则
,则.files/image285.gif) ∥
∥.files/image413.gif) ,
,
∴.files/image415.gif) 或其补角是异面直线
或其补角是异面直线.files/image285.gif) 与
与.files/image417.gif) 所成的角. ……………………2分
所成的角. ……………………2分
.files/image419.jpg) 设
设.files/image421.gif) ,则
,则.files/image423.gif) ,
,
.files/image425.gif) .
.
∴.files/image427.gif) . ………………………………4分
. ………………………………4分
∵在.files/image429.gif) 中,
中,.files/image431.gif) . ……5分
. ……5分
∴异面直线.files/image285.gif) 与
与.files/image417.gif) 所成的角为
所成的角为.files/image433.gif) . ……………………………6分
. ……………………………6分
(Ⅱ)连结.files/image435.gif) ,设
,设.files/image014.gif) 是
是.files/image438.gif) 的中点,过点
的中点,过点.files/image014.gif) 作
作.files/image441.gif) 于
于.files/image317.gif) ,连结
,连结.files/image444.gif) ,则
,则
.files/image446.gif) .又∵平面
.又∵平面.files/image448.gif) 平面
平面.files/image450.gif)
∴.files/image452.gif) 平面
平面.files/image450.gif) . ………………………………………………………8分
. ………………………………………………………8分
而.files/image454.gif) ∴
∴.files/image456.gif)
.files/image458.gif)
∴.files/image460.gif) 是二面角
是二面角.files/image462.gif) 的平面角. …………………………………9分
的平面角. …………………………………9分
由.files/image464.gif) =
=.files/image176.gif) ,
,.files/image467.gif) =
=.files/image176.gif) ,
,.files/image470.gif) ,得
,得.files/image472.gif) .……………10分
.……………10分
即二面角.files/image462.gif) 为
为.files/image475.gif)
∴所求二面角.files/image295.gif) 为
为.files/image478.gif)
.files/image475.gif) . ………………………………12分
. ………………………………12分
解法二:
(Ⅰ)如图分别以.files/image480.gif) 、
、.files/image438.gif) 、
、.files/image483.gif) 所在的直线为
所在的直线为.files/image227.gif) 轴、
轴、.files/image229.gif) 轴、
轴、.files/image487.gif) 轴建立空间直角坐标
轴建立空间直角坐标
系.files/image489.gif) . ……………………………………………………………………1分
. ……………………………………………………………………1分
设.files/image421.gif) ,则
,则.files/image491.gif) 、
、.files/image493.gif) 、
、.files/image495.gif) 、
、
.files/image497.gif) 、
、.files/image499.gif) .
………………………………………………………2分
.
………………………………………………………2分
∴.files/image501.gif) ,
,
∴.files/image503.gif) . ………………………5分
. ………………………5分
.files/image505.jpg) ∴异面直线
∴异面直线.files/image285.gif) 与
与.files/image417.gif) 所成的角为
所成的角为.files/image433.gif) .
………………………………………6分
.
………………………………………6分
(Ⅱ)由题意知点.files/image507.gif) ,设平面
,设平面.files/image509.gif) 的一个法向量为
的一个法向量为
.files/image511.gif) ,
,
则.files/image513.gif) , ∵
, ∵.files/image515.gif) ,
,
∴.files/image517.gif) ,取
,取.files/image519.gif) ,得
,得.files/image521.gif) . ………………8分
. ………………8分
易知平面.files/image523.gif) 的一个法向量
的一个法向量.files/image525.gif) ,
,
∴.files/image527.gif) .
…………………………………………11分
.
…………………………………………11分
∴二面角.files/image295.gif) 的大小为
的大小为.files/image530.gif) . …………………………12分
. …………………………12分
(21)解:(Ⅰ).files/image532.gif) , ………………………………………………2分
, ………………………………………………2分
依题意.files/image534.gif) ,即
,即.files/image536.gif) 解得
解得.files/image538.gif)
∴.files/image540.gif) ……………………………………………4分
……………………………………………4分
(Ⅱ)由(Ⅰ)知,曲线.files/image308.gif) 与
与.files/image310.gif) 有两个不同的
有两个不同的
交点,即.files/image544.gif) 在
在.files/image546.gif) 上有两个不同的实数解…5分
上有两个不同的实数解…5分
设.files/image548.gif)
.files/image550.gif) ,则
,则.files/image552.gif) , ………7分
, ………7分
由.files/image554.gif) 0的
0的.files/image556.gif) 或
或.files/image558.gif)
当.files/image560.gif) 时
时.files/image562.gif) ,于是
,于是.files/image564.gif) 在
在.files/image566.gif) 上递增;
上递增;
当.files/image568.gif) 时
时.files/image570.gif) ,于是
,于是.files/image564.gif) 在
在.files/image572.gif) 上递减. ………………9分
上递减. ………………9分
依题意有.files/image574.gif) . …………………11分
. …………………11分
∴实数.files/image054.gif) 的取值范围是
的取值范围是.files/image577.gif) . …………………………………12分
. …………………………………12分
(22)解:(Ⅰ)设点.files/image579.gif) ,由
,由.files/image581.gif) 得
得.files/image583.gif) . …………2分
. …………2分
由.files/image585.gif) ,得
,得.files/image587.gif) ,即
,即.files/image096.gif) . …………… 4分
. …………… 4分
又点.files/image317.gif) 在
在.files/image227.gif) 轴的正半轴上,∴
轴的正半轴上,∴.files/image592.gif) .故点
.故点.files/image320.gif) 的轨迹
的轨迹.files/image246.gif) 的方程是
的方程是
.files/image096.gif)
.files/image596.gif) . …………………………………………………………6分
. …………………………………………………………6分
(Ⅱ)由题意可知.files/image598.gif) 为抛物线
为抛物线.files/image246.gif) :
:.files/image096.gif) 的焦点,且
的焦点,且.files/image002.gif) 、
、.files/image004.gif) 为过焦点
为过焦点.files/image598.gif) 的直线与抛物
的直线与抛物
线.files/image246.gif) 的两个交点,所以直线
的两个交点,所以直线.files/image480.gif) 的斜率不为
的斜率不为.files/image606.gif) . ……………………………………7分
. ……………………………………7分
当直线.files/image480.gif) 斜率不存在时,得
斜率不存在时,得.files/image609.gif) ,不合题意; ……8分
,不合题意; ……8分
当直线.files/image480.gif) 斜率存在且不为
斜率存在且不为.files/image606.gif) 时,设
时,设.files/image612.gif) ,代入
,代入.files/image096.gif) 得
得
.files/image614.gif) ,
,
则.files/image616.gif) ,解得
,解得.files/image618.gif) . …………10分
. …………10分
代入原方程得.files/image620.gif) ,由于
,由于.files/image622.gif) ,所以
,所以.files/image624.gif) ,由
,由.files/image339.gif) ,
,
得.files/image627.gif) ,∴
,∴.files/image629.gif) . ……………………………………………………12分
. ……………………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com