
题目列表(包括答案和解析)
(本小题满分16分)
已知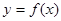 (
(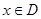 ,
,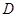 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数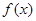
在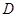 内单调递增或单调递减;②如果存在区间
内单调递增或单调递减;②如果存在区间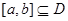 ,使函数
,使函数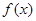 在区间
在区间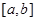 上的值域为
上的值域为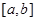 ,那么称
,那么称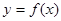 ,
,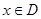 为闭函数。请解答以下问题:
为闭函数。请解答以下问题:
(1)判断函数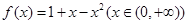 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(2)求证:函数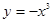 (
(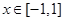 )为闭函数;
)为闭函数;
(3)若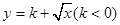 是闭函数,求实数
是闭函数,求实数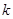 的取值范围.
的取值范围.
(本小题满分16分)
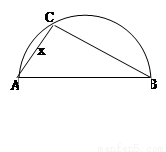
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(1)按下列要求建立函数关系式:
(i)设 (rad),将
(rad),将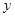 表示成
表示成 的函数;并写出函数的定义域. (5分)
的函数;并写出函数的定义域. (5分)
(ii)设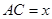 (km),将
(km),将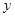 表示成
表示成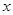 的函数;并写出函数的定义域. (5分)
的函数;并写出函数的定义域. (5分)
(2)请你选用(1)中的一个函数关系确定垃圾处理厂的位置,使建在此处的垃圾处理厂对城A和城B的总影响度最小? (6分)
(本小题满分16分,每小题8分)
求下列函数的值域:(1) 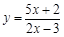 ;(2)
;(2) 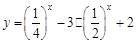 ,
,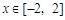 .
.
(本题满分16分)已知函数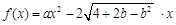 ,
,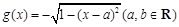 .
.
(1)当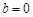 时,若
时,若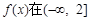 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对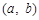 :存在
:存在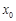 ,使得
,使得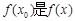 的最大值,
的最大值,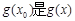 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对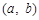 ,试构造一个定义在
,试构造一个定义在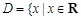 且
且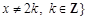 上的函数
上的函数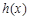 :使
:使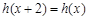 ,且当
,且当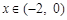 时,
时,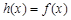 .
.
(本小题满分16分)某商品的市场需求量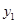 (万件)、市场供应量
(万件)、市场供应量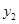 (万件)与市场价格x(元/件)分别近似的满足下列关系:
(万件)与市场价格x(元/件)分别近似的满足下列关系: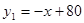 ,
,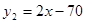 ,当
,当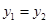 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加6万件,政府对每件商品应给予多少元补贴?
(3)求当每件商品征税6元时新的平衡价格?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com