练习册

  • 练习册
  • 试题
    故在的最大值为.故的最大值为 【查看更多】

     

    题目列表(包括答案和解析)

    已知函数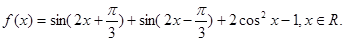

    （Ⅰ）求函数的最小正周期；

    （Ⅱ）求函数在区间上的最大值和最小值.

    【解析】（1）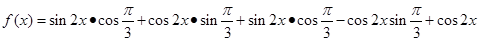

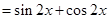
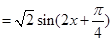    所以，的最小正周期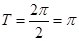

    （2）因为在区间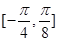上是增函数，在区间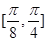上是减函数，

    又，，，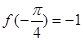

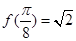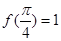    故函数在区间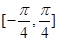上的最大值为，最小值为-1.

     

    查看答案和解析>>

    函数在同一个周期内，当 时,取最大值1，当时，取最小值。

    （1）求函数的解析式

    （2）函数的图象经过怎样的变换可得到的图象？

    （3）若函数满足方程求在内的所有实数根之和.

    【解析】第一问中利用

    又因

    又       函数

    第二问中，利用的图象向右平移个单位得的图象

    再由图象上所有点的横坐标变为原来的.纵坐标不变，得到的图象，

    第三问中，利用三角函数的对称性，的周期为

    在内恰有3个周期，

    并且方程在内有6个实根且

    同理，可得结论。

    解：(1)

    又因

    又       函数

    (2)的图象向右平移个单位得的图象

    再由图象上所有点的横坐标变为原来的.纵坐标不变，得到的图象，

    (3)的周期为

    在内恰有3个周期，

    并且方程在内有6个实根且

    同理，

    故所有实数之和为

     

    查看答案和解析>>

    针对酒后驾车经常造成的严重交通事故，国家质量监督检验检疫局2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准，新标准规定，驾驶人血液中的酒精含量大于（等于）20毫克/100毫升、小于80毫克/100毫升的行为属于饮酒驾车，含量大于（等于）80毫克/100毫升的行为属于醉酒驾车．经过测算一般情况下，成人饮用1杯啤酒后，血液中酒精浓度就可达到20mg/100ml，即构成饮酒驾驶的处罚条件．饮用2瓶啤酒或3两低度白酒后，血液酒精浓度可达到80mg/100ml，即构成醉酒驾驶处罚条件．
    经过统计成人在饮用2瓶啤酒或3两低度白酒后血液中酒精浓度随时间变化的函数为f(x)=
    a
    3
    x3-
    5
    2
    ax2+6ax+b，0.5≤x≤3
    k1
    x
    ，3＜x≤9
    k2e-
    9
    5
    x    ，x≥9

    现测得某人在饮酒后2小血液中酒精含量82，3小时含量68．（参考数据：e
    9
    5
    ≈
    411
    68
    ，e2.04≈
    137
    20
    ）
    （1）求a，b，k1，k2；
    （2）此人饮酒后血液中酒精浓度什么时候最大？最大值是多少？
    （3）此人经过多少时间可以驾车？

    查看答案和解析>>

    【答案】

    【解析】设，有几何意义知的最小值为， 又因为存在实数x满足，所以只要2大于等于f（x）的最小值即可．即2，解得：∈，所以a的取值范围是．故答案为：．

    查看答案和解析>>

    已知函数，.

    （Ⅰ）若函数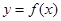依次在处取到极值.求的取值范围；

    （Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

    【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

    第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

    解：（1）

    ①

    （2）不等式 ，即，即.

    转化为存在实数，使对任意的，不等式恒成立.

    即不等式在上恒成立.

    即不等式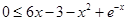在上恒成立.

    设，则.

    设，则，因为，有.

    故在区间上是减函数。又

    故存在，使得.

    当时，有，当时，有.

    从而在区间上递增，在区间上递减.

    又[来源:]

    所以当时，恒有；当时，恒有；

    故使命题成立的正整数m的最大值为5

     

    查看答案和解析>>


    同步练习册答案