
题目列表(包括答案和解析)
解:(1)由题意知,当![]() 、
、![]() 运动到
运动到![]() 秒时,如图①,过
秒时,如图①,过![]() 作
作![]() 交
交![]() 于
于![]() 点,则四边形
点,则四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ ![]() .解得
.解得![]() . 5分
. 5分
(2)分三种情况讨论:
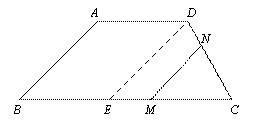
① 当![]() 时,如图②作
时,如图②作![]() 交
交![]() 于
于![]() ,则有
,则有![]() 即.
即.
 ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() . 6分
. 6分
② 当![]() 时,如图③,过
时,如图③,过![]() 作
作![]() 于H.
于H.
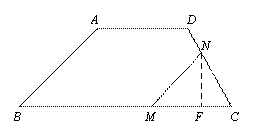 则
则![]() ,
,
∴![]() .
.
∴![]() .7分
.7分
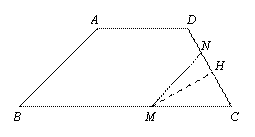
③ 当![]() 时,如图④.
时,如图④.
则![]() .
.
![]() . -------------------------------------8分
. -------------------------------------8分
综上所述,当![]() 、
、![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
 阅读理解
阅读理解
|
|

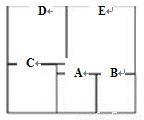
 如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积
如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积
解:设正方形A的边长为x厘米,则
正方形B的边长为_______ 厘米,
正方形C的边长为_______ 厘米
正方形D的边长为_______ 厘米,
正方形E的边长为_______ 厘米。
由题意可得方程:
解得 x=
答:长方形的面积为________ 平方厘米。
如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积
解:设正方形A的边长为x厘米,则
正方形B的边长为_______ 厘米,
正方形C的边长为_______ 厘米
正方形D的边长为_______ 厘米,
正方形E的边长为_______ 厘米。
由题意可得方程:
解得 x=
答:长方形的面积为________ 平方厘米。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com