
题目列表(包括答案和解析)
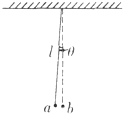
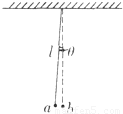
 用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.
用一根细线把小钢球悬挂起来.这叫做单摆,是最简单的振动系统.如题图所示,将小球稍微拉离平衡位置到达a然后放手,它就开始摆动.假如没有空气阻力,小球将一直摆下去.永不停止.仔细观察摆动过程,可以发现小球来回摆动一次所需的时问总是一样的,这是单摆的等时性,这个时问称为振动的周期.小明猜想单摆周期的大小可能与单摆的摆长l、偏离中心位置的夹角θ及摆球的质量m有关.于是小明做了分别改变单摆的摆长、偏离中心位置的夹角、摆球的质量的摆动实验,并测出了各种情形下单摆的周期,如下表.| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆长/m | 0.5 | 1 | 1.5 | 2 |
| 周期/s | 1.4 | 2 | 2.4 | 2.8 |
| 摆角θ | 1° | 2° | 3° | 4° |
| 周期/s | 2 | 2 | 2 | 2 |
| 摆球质量/g | 5 | 10 | 15 | 20 |
| 周期/s | 2 | 2 | 2 | 2 |
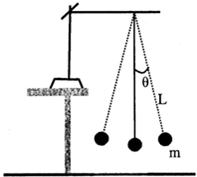 20、在研究摆钟的摆球摆动情况时,小菲和同学们观察摆钟后,利用如图所示的装置进行实验,测出了摆球摆动30次所用的时间,用这个时间除以30,得出摆球摆动一次所用时间.针对摆球摆动一次所用的时间与哪些因素有关这一问题,他们提出了以下猜想:
20、在研究摆钟的摆球摆动情况时,小菲和同学们观察摆钟后,利用如图所示的装置进行实验,测出了摆球摆动30次所用的时间,用这个时间除以30,得出摆球摆动一次所用时间.针对摆球摆动一次所用的时间与哪些因素有关这一问题,他们提出了以下猜想:| 次数 | 摆线长 L/m |
摆球质量 m/g |
摆角θ/° | 摆动一次的 时间t/s |
| 1 | 1 | 20 | 3° | 2 |
| 2 | 1.4 | 20 | 3° | 2.4 |
| 3 | 1.4 | 20 | 5° | 2.4 |
| 4 | 1.4 | 30 | 5° | 2.4 |
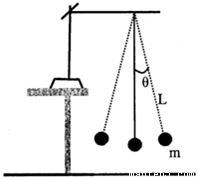 在研究摆钟的摆球摆动情况时,小菲和同学们观察摆钟后,利用如图所示的装置进行实验,测出了摆球摆动30次所用的时间,用这个时间除以30,得出摆球摆动一次所用时间.针对摆球摆动一次所用的时间与哪些因素有关这一问题,他们提出了以下猜想:
在研究摆钟的摆球摆动情况时,小菲和同学们观察摆钟后,利用如图所示的装置进行实验,测出了摆球摆动30次所用的时间,用这个时间除以30,得出摆球摆动一次所用时间.针对摆球摆动一次所用的时间与哪些因素有关这一问题,他们提出了以下猜想:| 次数 | 摆线长 L/m | 摆球质量 m/g | 摆角θ/° | 摆动一次的 时间t/s |
| 1 | 1 | 20 | 3° | 2 |
| 2 | 1.4 | 20 | 3° | 2.4 |
| 3 | 1.4 | 20 | 5° | 2.4 |
| 4 | 1.4 | 30 | 5° | 2.4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com