
题目列表(包括答案和解析)
(08年杨浦区测试)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,
(1)求![]() 的值.
的值.
(2)当![]() 时,在数列
时,在数列![]() 中是否存在一项
中是否存在一项![]() (
(![]() 正整数),使得
正整数),使得 ![]() ,
,![]() ,
,![]() 成等比数列,若存在,求
成等比数列,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)若自然数![]() (
(![]() 为正整数)
为正整数)
满足![]() <
< ![]() <
<![]() <
< ![]() <
< ![]() <
<![]() , 使得
, 使得![]() 成等比数列,
成等比数列,
(文科考生做)当![]() 时, 用
时, 用![]() 表示
表示![]() .
.
(理科考生做)求![]() 的所有可能值.
的所有可能值.
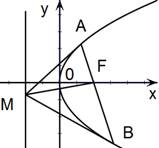
(08年杨浦区测试)设抛物线![]() 的焦点为
的焦点为![]() ,经过点
,经过点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() 是抛物线的准线上的一点,
是抛物线的准线上的一点,![]() 是坐标原点.若直线
是坐标原点.若直线![]() 、
、![]() 、
、![]() 的斜率分别记为:
的斜率分别记为:![]() 、
、![]() 、
、![]() ,(如图)
,(如图)
(1)若![]() ,求抛物线的方程.
,求抛物线的方程.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)如果取![]() ,
,![]() 时,
时,
(文科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
(理科考生做)判定![]() 和
和![]() 的值大小关系.并说明理由.
的值大小关系.并说明理由.
通过你对以上问题的研究,请概括出在怎样的更一般的条件下,使得你研究的结果(即![]() 和
和![]() 的值大小关系)不变,并证明你的结论.
的值大小关系)不变,并证明你的结论.
|
| x2 |
| 4 |
|
| π |
| 2 |
(1)若两人各做一次实验,求至少有一人实验成功的概率;
(2)若乙单独做三次实验,求恰有两次成功的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com