（2013•湛江二模）某市甲、乙两校高二级学生分别有1100人和1000人，为了解两校全体高二级学生期末统考的数学成绩情况，采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩，并得到成绩频数分布表如下，规定考试成绩在[120，150]为优秀．
甲校：

分组	[70，80）	[80，90）	[90，100）	[100，110）	[110，120）	[120，130）	[130，140）	[140，150）
频数	2	3	10	15	15	x	3	1

乙校：

分组	[70，80）	[80，90）	[90，100）	[100，110）	[110，120）	[120，130）	[130，140）	[140，150）
频数	1	2	9	8	10	10	y	3

（1）求表中x与y的值；
（2）由以上统计数据完成下面2x2列联表，问是否有99%的把握认为学生数学成绩优秀与所在学校有关？

	甲校	乙校	总计
优秀
非优秀
总计

高二年级某三个班级参加“深圳市第二高级中学第一届数学竞赛”分别有1，2，3名同学获奖，并站成一排合影留念，若相同班级的同学不能相邻，则有（　　）种排法．

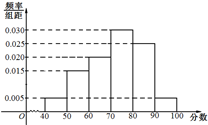某校从参加高三年级期末统考测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
（Ⅰ）估计这次测试数学成绩的平均分和众数；
（Ⅱ）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为ξ，求ξ的分布列及数学期望Eξ．

（2013•鹰潭一模）某校在高三年级上学期期末考试数学成绩中抽取n个数学成绩进行分析，全部介于80分与130分之间，将测试结果按如下方式分成五组，第一组[80，90）；第二组[90，100）…第五组[120，130]，下表是按上述分组方法得到的频率分布表：

分 组	频 数	频 率
[80，90）	x	0.04
[90，100）	9	y
[100，110）	z	0.38
[110，120）	17	0.34
[120，130]	3	0.06

（1）求n及分布表中x，y，z的值；
（2）校长决定从第一组和第五组的学生中随机抽取2名进行交流，求第一组至少有一人被抽到的概率．
（3）设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m，n，求事件“|m-n|＞10”的概率．

（2012•济宁一模）2014年山东省第二十三届运动会将在济宁召开，为调查我市某校高中生是否愿意提供志愿者服务，用简单随机抽样方法从该校调查了50人，结果如下：K

是否愿意提供志愿者服务 性别	愿意	不愿意
男生	20	5
女生	10	15

（I）用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人，其中男生抽取多少人？
（II）在（I）中抽取的6人中任选2人，求恰有一名女生的概率；
（III）你能否有99%的把握认为该校高中生是否愿意提供志愿者服务与性别有关？
下面的临界值表供参考：

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

独立性检验统计量K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d．