
题目列表(包括答案和解析)
关于函数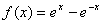 的性质说法正确的是 ( )
的性质说法正确的是 ( )
A.奇函数且在R上为增函数 B.奇函数且在R上为减函数
C.偶函数且在R上为增函数 D.偶函数且在R上为减函数
 |
| y |
 |
| y |
下列说法正确的是 。
(1)从匀速传递的产品生产流水线上,质检人员每20分钟从中抽取一件产品进行检测,这样的抽样方法为分层抽样;
(2)两个随机变量相关性越强,相关系数 的绝对值越接近1,若
的绝对值越接近1,若 或
或 时,则
时,则 与
与 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
(3)在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)对于回归直线方程 ,当
,当 每增加一个单位时,
每增加一个单位时, 平均增加12个单位;
平均增加12个单位;
(5)已知随机变量 服从正态分布
服从正态分布
 ,若
,若 ,则
,则 。
。
下列说法正确的是 。
(1)从匀速传递的产品生产流水线上,质检人员每20分钟从中抽取一件产品进行检测,这样的抽样方法为分层抽样;
(2)两个随机变量相关性越强,相关系数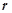 的绝对值越接近1,若
的绝对值越接近1,若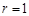 或
或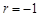 时,则
时,则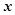 与
与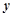 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
(3)在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
(4)对于回归直线方程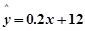 ,当
,当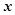 每增加一个单位时,
每增加一个单位时,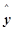 平均增加12个单位;
平均增加12个单位;
(5)已知随机变量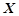 服从正态分布
服从正态分布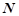
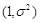 ,若
,若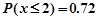 ,则
,则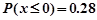 。
。
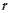 的绝对值越接近1,若
的绝对值越接近1,若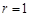 或
或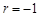 时,则
时,则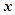 与
与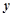 的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;
的关系完全对应(即有函数关系),在散点图上各个散点均在一条直线上;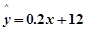 ,当
,当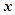 每增加一个单位时,
每增加一个单位时,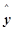 平均增加12个单位;
平均增加12个单位;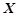 服从正态分布
服从正态分布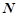
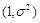 ,若
,若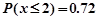 ,则
,则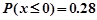 。
。
说明:
一、本解答给出一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则。
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得累加分。
四、只给整数分数,选择题和填空题不给中间分数。
一、选择题:每小题5分,满分60分。
1―5 DBADD 6―10 AAACA 11―12 BC
二、填空题:每题5分,共20分
13. 14.14 15.1 16.②③
14.14 15.1 16.②③
三、解答题(满分70分)
17.本小题主要考查正弦定理、余弦定理,三角形面积公式等基础知识。
解:(1)
 (5分)
(5分)
(2)

得 (8分)
(8分)
 (10分)
(10分)
18.本小题主要考查概率的基本知识与分类思想,独立重复试验概率问题,考查运用数学知
识分析问题解决问题的能力。
解:(1)需赛七局结束比赛说明前六局3:3打平,即在第三、第四、第五、第六局中乙恰赢一局,设需赛七局结束比赛为事件A,
则 (5分)
(5分)
(2)设甲获胜为事件B,则甲获胜包括甲以4:2获胜和甲以4:3获胜两种情况:

 (12分)
(12分)
19.本小题主要考查正四棱柱中线线位置关系、线面垂直判定、三垂线定理、二面角等基础知识,考查空间想象能力、逻辑思维能力、运算能力以及空间向量的应用。
|