
题目列表(包括答案和解析)
(08年昆明市适应考试)(12分)设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() :
:![]() 相切. 记动圆的圆心
相切. 记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),
为切点),
证明:直线![]() 必过定点并指出定点坐标.
必过定点并指出定点坐标.
(09年莱西一中模拟文)(12分)
设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() :
:![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为直线
为直线![]() 上的动点,过点
上的动点,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() (
(![]() 为切点),
为切点),
证明:直线![]() 必过定点并指出定点坐标.
必过定点并指出定点坐标.
[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A.  选修4-1:几何证明选讲
选修4-1:几何证明选讲
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
B. 选修4-2:矩阵与变换
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
C. 选修4-4:坐标系与参数方程
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
D. 选修4-5:不等式选讲
设a、b是非负实数,求证: 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指定区域答题。如果多做,则按所做的第一题计分。)
22.选修4-1:几何证明选讲
如图,已知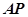 是⊙
是⊙ 的切线,
的切线,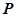 为切点,
为切点,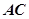 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于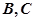 两点,圆心
两点,圆心 在
在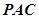 的内部,点
的内部,点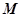 是
是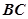 的中点。
的中点。
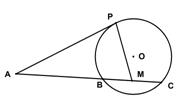
(1)证明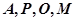 四点共圆;
四点共圆;
(2)求 的大小。
的大小。
23.选修4—4:坐标系与参数方程[来源:ZXXK]
已知直线 经过点
经过点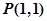 ,倾斜角
,倾斜角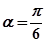 。
。
(1)写出直线 的参数方程;
的参数方程;
(2)设 与曲线
与曲线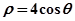 相交于两点
相交于两点 ,求点
,求点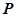 到
到 两点的距离之积。
两点的距离之积。
24.选修4—5:不等式证明选讲
若不等式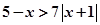 与不等式
与不等式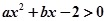 同解,而
同解,而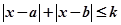 的解集为空集,求实数
的解集为空集,求实数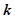 的取值范围。
的取值范围。
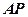 是⊙
是⊙ 的切线,
的切线,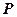 为切点,
为切点,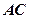 是⊙
是⊙ 的割线,与⊙
的割线,与⊙ 交于
交于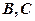 两点,圆心
两点,圆心 在
在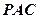 的内部,点
的内部,点
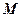 是
是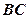 的中点。
的中点。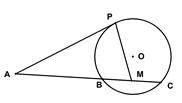
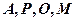 四点共圆;
四点共圆;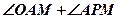 的大小。
的大小。 经过点
经过点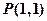 ,倾斜角
,倾斜角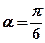 。
。 的参数方程;
的参数方程; 与曲线
与曲线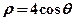 相交于两点
相交于两点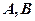 ,求点
,求点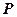 到
到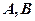 两点的距离之积。
两点的距离之积。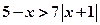 与不等式
与不等式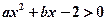 同解,而
同解,而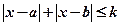 的解集为空集,求实数
的解集为空集,求实数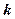 的取值范围。
的取值范围。一、选择题(每小题5分,共60分)
1.D 2.A 3.D 4.D 5.A 6.C 7.B 8.B 9.C 10.A 11.C 12.B
二、填空题(每小题5分,共20分)
13.2 14. 15.
15. 16.③④
16.③④
三、解答题(共70分)
17.(本小题满分10分)
解:(Ⅰ)由 可得:
可得:
 又
又
 .
--------------------------------5分
.
--------------------------------5分
(Ⅱ) ,
,

 .
---------------------------------10分
.
---------------------------------10分
18.(本小题满分12分)
解: 设A队得分为2分的事件为 ,
,
(Ⅰ)∴ .
------------------4分
.
------------------4分
(Ⅱ)设A队得分不少于2分的事件为M , B队得分不多于2分的事件为N,
由(Ⅰ)得A队得分为2分的事件为 , A队得分为3分的事件为
, A队得分为3分的事件为 ,
,
B队得分为3分的事件为 ,
,
∴ - ----------------- 9分
- ----------------- 9分
 .
------------------ 12分
.
------------------ 12分
19.(本小题满分12分)
解法一、
(Ⅰ)连结 交
交 于点O,
于点O,
∵ 平面
平面 ,平面
,平面 ∩平面
∩平面
∴
 又∵
又∵ 是
是 的中点
的中点
∴  是
是 的中点.
------------------6分
的中点.
------------------6分
(Ⅱ)作 ,垂足为
,垂足为 ,连结
,连结
 面
面


 平面
平面
∴ 是
是 在平面
在平面 上的射影
上的射影
∴
∴ 是二面角
是二面角 的平面角
的平面角
∵ ,
,

在直角三角形 中,
中,
 ,
,
 二面角
二面角 的大小为
的大小为 . ------------------12分
. ------------------12分
解法二、
 (Ⅰ)建立如图所示空间坐标系
(Ⅰ)建立如图所示空间坐标系
则 ,
, 

平面 的法向量为
的法向量为 由
由
 得
得 ,
,
 平面
平面 ,
,
 .
.
所以点 是棱
是棱 的中点.
的中点.
(Ⅱ)平面 的法向量
的法向量 ,设平面
,设平面 的法向量为
的法向量为 . 则
. 则

 二面角
二面角 的大小为
的大小为 .
.
20.(本小题满分12分)
解:(Ⅰ)由 得:
得: ,所以等差数列
,所以等差数列 的通项公式为
的通项公式为

 . ------------------------4分
. ------------------------4分
(Ⅱ)由 得:
得:


从而
故数列 是单调递增的数列,又因
是单调递增的数列,又因 是
是 中的最小项,要使
中的最小项,要使 恒成立,
恒成立,
则只需 成立即可,由此解得
成立即可,由此解得 ,由于
,由于 ∈
∈ ,
,
故适合条件的 的最大值为1. ------------------------12分
的最大值为1. ------------------------12分
21.(本小题满分12分)
解:(Ⅰ) ,
,  是奇函数,其图象关于原点对称,
是奇函数,其图象关于原点对称,
所以函数图象的对称中心 即为
即为
 .
-----------------2分
.
-----------------2分
 ,其图象顶点坐标为
,其图象顶点坐标为
所以函数 图象的对称中心与导函数
图象的对称中心与导函数 图象的顶点横坐标相同. -----------------4分
图象的顶点横坐标相同. -----------------4分
(Ⅱ)令 得
得 .
.
当 变化时,
变化时, 变化情况如下表:
变化情况如下表:








0

0



极大值

极小值

 时,
时, 有极大值2,
有极大值2,
 ,曲线
,曲线 在点
在点 处的切线的斜率
处的切线的斜率 .
.
直线 的方程为
的方程为 -----------------6分
-----------------6分
曲线 在点
在点 处的切线的斜率
处的切线的斜率 .
.
直线 的方程为
的方程为
又曲线 在点
在点 处的切线的斜率
处的切线的斜率 .
.
直线 的方程为
的方程为 .
.
联立直线 的方程与直线
的方程与直线 的方程,
的方程,  ,解得
,解得 ,
,
 .-----------------10分
.-----------------10分
 联立直线
联立直线 的方程与直线
的方程与直线 的方程,
的方程,  ,解得
,解得 ,
,
 .
.
 ,
,
所以 . -----------------12分
. -----------------12分
图象如右:
22.(本小题满分12分)
解:(Ⅰ)过点 作
作 垂直直线
垂直直线 于点
于点
依题意得: ,
,
所以动点 的轨迹为是以
的轨迹为是以 为焦点,直线
为焦点,直线 为准线的抛物线,
为准线的抛物线,
即曲线 的方程是
的方程是 ---------------------4分
---------------------4分
(Ⅱ)解法一:设 、
、 、
、 ,则
,则
由 知,
知, , ∴
, ∴ ,
,
又∵切线AQ的方程为: ,注意到
,注意到
切线AQ的方程可化为: ,
,
由 在切线AQ上, ∴
在切线AQ上, ∴
所以点 在直线
在直线 上;
上;
同理,由切线BQ的方程可得: .
.
所以点 在直线
在直线 上;
上;
可知,直线AB的方程为: ,
,
即直线AB的方程为: ,
,
∴直线AB必过定点 .
------------------------12分
.
------------------------12分
(Ⅱ)解法二:设 ,切点的坐标为
,切点的坐标为 ,则
,则
由 知,
知, ,得切线方程:
,得切线方程: .
.
即为: ,又∵
,又∵ 在切线上,
在切线上,
所以可得: ,解之得:
,解之得: .
.
所以切点 ,
,
∴ .
.
故直线AB的方程为:
化简得:
即直线AB的方程为:
∴直线AB必过定点 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com