
题目列表(包括答案和解析)
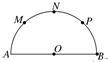 如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点
如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点| 2 |
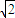 的概率.
的概率.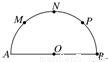
如图,已知AB是半圆O的直径,弦AD、BC相交于点P,那么![]() 等于
等于

sin∠BPD
cos∠BPD
tan∠BPD
cot∠BPD
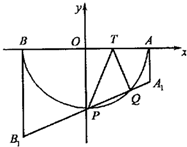 已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.
已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.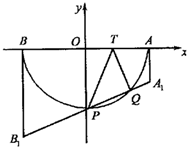 已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.
已知T是半圆O的直径AB上一点,AB=2,OT=t(0<t<1).以AB为腰的直角梯形AA1B1B中,AA1垂直于AT,且|AA1|=|AT|,BB1垂直于BT,且|BB1|=|BT|,A1B1交半圆于P,Q两点,建立如图所示直角坐标系,O为坐标原点.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com