
题目列表(包括答案和解析)
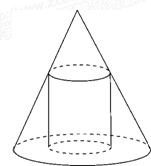 已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.
已知一个圆锥的底面半径为R,高为H,在其中有一个高为x的内接圆柱. 如图所示.| x | H |
 已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.
已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.| π |
| 2 |
| π |
| 4 |
 如图所示高脚杯的轴截面是方程为x2=2py(p>0)的抛物线,现放一半径为r小球到高脚杯中,若小球能落到杯子底部,则小球的半径r的取值范围为
如图所示高脚杯的轴截面是方程为x2=2py(p>0)的抛物线,现放一半径为r小球到高脚杯中,若小球能落到杯子底部,则小球的半径r的取值范围为 );
);
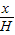 );
);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com