
题目列表(包括答案和解析)
已知三棱锥A-BCD内接于球O,AB=AD=AC=BD=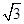 ,∠BCD=60°,则球O的表面积为
,∠BCD=60°,则球O的表面积为
A.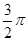 B.
B.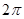 C.
C.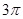 D.
D.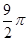
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
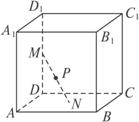
(08年长郡中学一模文)(12分)如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面![]() 内作菱形ABCD,边长为1,∠BAD=60°,再在面
内作菱形ABCD,边长为1,∠BAD=60°,再在面![]() 的上方,分别以△
的上方,分别以△![]() 与△
与△![]() 为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.
(Ⅰ)求证:PQ⊥BD;
(Ⅱ)求二面角P-BD-Q的余弦值;
(Ⅲ)求点P到平面QBD的距离;

如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
 ①
① ;
;
②∠BAC=60°;
③三棱锥D—ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
(本题满分14分).如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=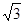 .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD 于H点,判定H点位于平面ABCD的那个具体位置?(无须证明)
(Ⅲ)求二面角A-BE-P的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com