
题目列表(包括答案和解析)
解析:y=log0.5(1-x)在(0,1)上为增函数;
y=x0.5在(0,1)上是增函数;
y=0.51-x在(0,1)上为增函数;
函数y=![]() (1-x2)在(-∞,0)上为增函数,在(0,+∞)上为减函数,
(1-x2)在(-∞,0)上为增函数,在(0,+∞)上为减函数,
∴函数y=![]() (1-x2)在(0,1)上是减函数.
(1-x2)在(0,1)上是减函数.
答案:D
解析:由题意知
当-2≤x≤1时,f(x)=x-2,
当1<x≤2时,f(x)=x3-2,
又∵f(x)=x-2,f(x)=x3-2在定义域上都为增函数,
∴f(x)的最大值为f(2)=23-2=6.
答案:C
解析:依题意可得对称轴x=![]() =1,∴a=5.
=1,∴a=5.
答案:C
解析:依题意得f(x)的图象关于直线x=1对称,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函数f(x)是以4为周期的函数.由f(x)在[3,5]上是增函数与f(x)的图象关于直线x=1对称得,f(x)在[-3,-1]上是减函数.又函数f(x)是以4为周期的函数,因此f(x)在[1,3]上是减函数,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
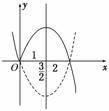 解析:y=-(x-3)|x|
解析:y=-(x-3)|x|
=![]()
作出该函数的图象,观察图象知递增区间为[0,![]() ].
].
答案:[0,![]() ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com