
题目列表(包括答案和解析)

| 3 |
| 3 |


图20
(1)在丙图中画出感应电流随时间变化的it图象(以逆时针方向为正);
(2)求出线框中感应电流的有效值.
如图甲所示,在周期性变化的匀强磁场区域内有垂直于磁场的一半径为r = 1m、电阻为R = 3.14Ω的金属圆形线框,当磁场按图乙所示规律变化时,线框中有感应电流产生。
(1)在丙图中画出感应电流随时间变化的![]() 图象(以逆时针方向为正)
图象(以逆时针方向为正)
(2)求出线框中感应电流的有效值
 |
如图a所示,一个电阻值为R=1Ω,匝数为n=100的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1=12cm. 在线圈中半径为r2=10cm的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图b所示。图线与横、纵轴的截距分别为t0=10s和B0=3T. 导线的电阻不计。求0至t1=6s的时间内
(a)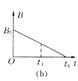
(1)通过电阻R1上的电流大小和方向;
(2)通过电阻R1上的电量q及电阻R1上产生的热量。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com