dyr232
三、解答题.(12×5+10=70分,答案写在答题纸的答题区内.)
17.(Ⅰ)∵ m?n ………
2分
………
2分
∴ ,解得
,解得 ………
6分
………
6分
(Ⅱ) ………
8分
………
8分
∵ ,∴
,∴ ………10分
………10分
∴ 的值域为[
的值域为[ ] ………12分
] ………12分
18.(Ⅰ)把一根长度为8的铁丝截成3段,且三段的长度均为整数,共有21种解法.
(可视为8个相同的小球放入3个不同盒子,有 种方法) … 3分
种方法) … 3分
其中能构成三角形的情况有3种情况:“2,3,3”、“3,2,3”、“3,3,2”.
则所求的概率是 ………
6分
………
6分
(Ⅱ)根据题意知随机变量 ………
8分
………
8分
∴ ……12分
……12分
19.(Ⅰ)∵点A、D分别是 、
、 的中点,∴
的中点,∴ . …… 2分
. …… 2分
∴∠ =90º.∴
=90º.∴ .∴
.∴  ,
,
∵ ,∴
,∴ ⊥平面
⊥平面 . ………
4分
. ………
4分
∵ 平面
平面 ,∴
,∴ . ……… 5分
. ……… 5分
 (Ⅱ)建立如图所示的空间直角坐标系
(Ⅱ)建立如图所示的空间直角坐标系 .
.
则 (-1,0,0),
(-1,0,0), (-2,1,0),
(-2,1,0), (0,0,1).
(0,0,1).
∴ =(-1,1,0),
=(-1,1,0), =(1,0,1), …6分
=(1,0,1), …6分
设平面 的法向量为
的法向量为 =(x,y,z),则:
=(x,y,z),则:
 ,
……… 8分
,
……… 8分
令 ,得
,得 ,∴
,∴ =(1,1,-1)
=(1,1,-1)
显然, 是平面
是平面 的一个法向量,
的一个法向量, =(
=(
 ). ………10分
). ………10分
∴cos< ,
, >=
>= .
.
∴二面角 的平面角的余弦值是
的平面角的余弦值是 .
………12分
.
………12分
20.(Ⅰ) ………
4分
………
4分
(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等………
5分
⑴当P在y轴上时,易知R在x轴上,此时PR方程为 ,
,

 . ………
6分
. ………
6分
⑵当P在x轴上时,易知R在y轴上,此时PR方程为 ,
,

 . ………
7分
. ………
7分
⑶当P不在坐标轴上时,设PQ斜率为k, 、
、
P在椭圆上, .......①;R在椭圆上,
.......①;R在椭圆上, ....
....
②利用Rt△POR可得  ………
9分
………
9分
即 
整理得  . ………11分
. ………11分
再将①②带入,得
综上当 时,有
时,有 . ………12分
. ………12分
21.(Ⅰ) 时,
时, 单调递减,
单调递减,
当 单调递增。
单调递增。
①若 无解;
无解;
②若

③若 时,
时, 上单调递增,
上单调递增,
 ;
;
所以 ……… 4分
……… 4分
(Ⅱ) 则
则
设 则
则 时,
时,
 单调递减,
单调递减, 单调递增,
单调递增,
所以 因为对一切
因为对一切
恒成立,所以 ; ………
8分
; ………
8分
(Ⅲ)问题等价于证明 ,
,
由(Ⅰ)可知
当且仅当 时取到,设
时取到,设
则 ,当且仅当
,当且仅当 时取到,
时取到,
从而对一切 成立. ………12分
成立. ………12分
22.(Ⅰ)连接OC,∵OA=OB,CA=CB ∴OC⊥AB∴AB是⊙O的切线 …
5分
(Ⅱ)∵ED是直径,∴∠ECD=90°∴∠E+∠EDC=90°
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,∴∠BCD=∠E
又∵∠CBD+∠EBC,∴△BCD∽△BEC ∴ ∴BC2=BD•BE
∴BC2=BD•BE
∵tan∠CED= ,∴
,∴ ∵△BCD∽△BEC, ∴
∵△BCD∽△BEC, ∴
设BD=x,则BC=2 又BC2=BD•BE,∴(2x)2=x•(x+6)
解得x1=0,x2=2, ∵BD>0, ∴BD=2∴OA=OB=BD+OD=3+2=5 … 10分
23.(Ⅰ) …
5分
…
5分
(Ⅱ) … 10分
… 10分
23.(Ⅰ) ,
, …
5分
…
5分
(Ⅱ)
 … 10分
… 10分

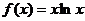 .
.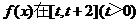 上的最小值;
上的最小值;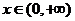 ,都有
,都有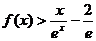 成立.
成立.