
题目列表(包括答案和解析)
小明在《高中全程复习优化训练》中遇到这样一道习题,无法确定答案,请你帮他解决.题目为:下列结论中正确的个数是
①方程(x-1)3(x+5)(x+1)=0的解集为{1,1,1,-5,-1};②实数集{1,a,a2-a}中元素a所满足的条件为a≠0且a≠1且a≠2;③集合A={a,b,c}中的三个元素可构成△ABC三边长,则△ABC一定不是等腰三角形;④方程组 的解集为{(3,1,4)};⑤集合N中的最小元素为1;⑥方程(x-1)3(x+2)(x-5)=0的解集含有3个元素;⑦0∈
的解集为{(3,1,4)};⑤集合N中的最小元素为1;⑥方程(x-1)3(x+2)(x-5)=0的解集含有3个元素;⑦0∈![]() ;⑧满足1+x>x的实数的全体形成集合.
;⑧满足1+x>x的实数的全体形成集合.
A.3
B.4
C.5
D.6
已知 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:
上的函数,其图象是一条连续的曲线,且满足下列条件:
① 的值域为M,且MÍ
的值域为M,且MÍ ;
;
②对任意不相等的 ,
, ∈
∈ , 都有|
, 都有| -
- |<|
|<| -
- |.
|.
那么,关于 的方程
的方程 =
= 在区间
在区间 上根的情况是
( )
上根的情况是
( )
A.没有实数根 B.有且仅有一个实数根
C.恰有两个不等的实数根 D.实数根的个数无法确定
已知![]() 是定义在
是定义在![]() 上的函数,其图象是一条连续的曲线,且满足下列条件:
上的函数,其图象是一条连续的曲线,且满足下列条件:
①![]() 的值域为M,且MÍ
的值域为M,且MÍ![]() ;
;
②对任意不相等的![]() ,
,![]() ∈
∈![]() , 都有|
, 都有|![]() -
-![]() |<|
|<|![]() -
-![]() |.
|.
那么,关于![]() 的方程
的方程![]() =
=![]() 在区间
在区间![]() 上根的情况是 ( )
上根的情况是 ( )
A.没有实数根 B.有且仅有一个实数根
C.恰有两个不等的实数根 D.实数根的个数无法确定
已知 是定义在
是定义在 上的函数,其图象是一条连续的曲线,且满足下列条件:
上的函数,其图象是一条连续的曲线,且满足下列条件:
① 的值域为M,且MÍ
的值域为M,且MÍ ;
;
②对任意不相等的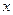 ,
, ∈
∈ , 都有|
, 都有| -
- |<|
|<|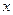 -
- |.
|.
那么,关于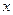 的方程
的方程 =
=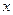 在区间
在区间 上根的情况是 ( )
上根的情况是 ( )
| A.没有实数根 | B.有且仅有一个实数根 |
| C.恰有两个不等的实数根 | D.实数根的个数无法确定 |
已知f(x)是定义在[a,b]上的函数,其图象是一条连续的曲线,且满足下列条件:
①f(x)的值域为M,且M![]() [a,b];
[a,b];
②对任意不相等的x,y∈[a,b],都有|f(x)-f(y)|<|x-y|.
那么,关于x的方程f(x)=x在区间[a,b]上根的情况是
没有实数根
有且仅有一个实数根
恰有两个不等的实数根
实数根的个数无法确定
一、选择题:每小题5分,满分60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
A
A
A
B
D
D
B
C
C
二、填空题:每小题5分,满分20分.
13.
14. 
15.
16.①③④
 三、解答题
三、解答题
17.设两个实数为a,b, ,
, ,建立平面直角坐标系aOb, 则点
,建立平面直角坐标系aOb, 则点 在正方形OABC内 ………
2分
在正方形OABC内 ………
2分
(Ⅰ) 记事件A“两数之和小于 ,则满足条件的点
,则满足条件的点 在多边形OAEFC内
在多边形OAEFC内
所以 ………
6分
………
6分
(Ⅱ) 记事件B“两数的平方和小于 在扇形内
在扇形内
所以 ………10分
………10分
18.∵m?n ∴
∴ ………
4分
………
4分
再由余弦定理 得:
得:
(Ⅰ)由 得
得 ,故
,故 ………
8分
………
8分
(Ⅱ)由 得
得
解得 ,所以
,所以 的取值范围是
的取值范围是 ………12分
………12分
19.(Ⅰ)连接 ,交
,交 于
于 ,易知
,易知 为
为 、
、 中点,故在△
中点,故在△ 中,
中, 为边
为边 的中位线,故
的中位线,故 ∥
∥ ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 ∥平面
∥平面 ……… 5分
……… 5分
(Ⅱ)在平面 内过点
内过点 作
作 ⊥
⊥ ,垂足为H,
,垂足为H,
∵平面 ⊥平面
⊥平面 ,且平面
,且平面 ∩平面
∩平面
 ,
,
∴ ⊥平面
⊥平面 ,∴
,∴ ⊥
⊥ , ……… 8分
, ……… 8分
又∵ ,
, 为
为 中点,∴
中点,∴ ⊥
⊥
∴ ⊥平面
⊥平面 ,∴
,∴ ⊥
⊥ ,又∵
,又∵ ,
,
∴ ⊥平面
⊥平面 . ………12分
. ………12分
20.(Ⅰ)∵ 是各项均为正数的等差数列,且公差
是各项均为正数的等差数列,且公差
∴ ∴
∴ ………
3分
………
3分
∴ 为常数,∴
为常数,∴ 是等差数列 ……… 5分
是等差数列 ……… 5分
(Ⅱ)∵ ,∴
,∴
∴ 是公差为1的等差数列 ………
7分
是公差为1的等差数列 ………
7分
∴ ,∴
,∴ ………
9分
………
9分
当 时,
时, ………10分
………10分
当 时,
时,
综上, ………12分
………12分
21.(Ⅰ) ………
4分
………
4分
(Ⅱ)由椭圆的对称性知:PRQS为菱形,原点O到各边距离相等……… 5分
⑴当P在y轴上时,易知R在x轴上,此时PR方程为 ,
,

 . ………
6分
. ………
6分
⑵当P在x轴上时,易知R在y轴上,此时PR方程为 ,
,

 . ………
7分
. ………
7分
⑶当P不在坐标轴上时,设PQ斜率为k, 、
、
P在椭圆上, .......①;R在椭圆上,
.......①;R在椭圆上, ......②
......②
利用Rt△POR可得  ………
9分
………
9分
即 
整理得  . ………11分
. ………11分
再将①②带入,得
综上当 时,有
时,有 . ………12分
. ………12分
22.(Ⅰ)∵ ,且
,且 ,∴
,∴
∴在 上,
上,  和
和 变化情况如下表:
变化情况如下表:
x


0

1

+
0
-


↑
b
↓

……… 2分
∵函数 在
在 上的最大值为1,
上的最大值为1,
∴ ,此时应有
,此时应有 ∴
∴
∴ ,
, ………
4分
………
4分
(Ⅱ) ………
6分
………
6分
所求切线方程为 ………
8分
………
8分
(Ⅲ) ………10分
………10分
设
△
∴当 时,函数
时,函数 的无极值点
的无极值点
当 时,函数
时,函数 有两个极值点 ………12分
有两个极值点 ………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com