已知在上是增函数，在上是减函数，且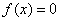有三个根（。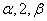

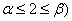（I）求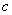的值，并求出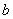和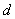的取值范围；

（Ⅱ）求证：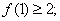

（Ⅲ）求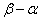的取值范围，并写出当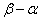取最小值时的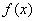的解析式。

 

 

 

 

 

 

 

 

 

 

 

 

函数，则下列命题正确的是                             （      ）

A．若在和上是增函数，则是增函数；

B．若在和上是减函数，则是减函数；
C。若是偶函数，在上是增函数，则在上也是增函数；

D．若是奇函数，在上是增函数，则在上也是增函数。

函数f(x)，g(x)，h(x)的定义域和值域都是实数集R，且f(x)为增函数，g(x)，h(x)为减函数，则在R上，f[g(x)]是________函数；g[h(x)]是________函数；h[f(x)]是________函数．

设函数

（1）当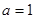时，求曲线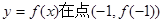处的切线方程；

（2）当时，求的极大值和极小值；

（3）若函数在区间上是增函数，求实数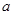的取值范围.

【解析】（1）中，先利用，表示出点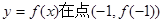的斜率值这样可以得到切线方程。（2）中，当，再令，利用导数的正负确定单调性，进而得到极值。（3）中，利用函数在给定区间递增，说明了在区间导数恒大于等于零，分离参数求解范围的思想。

解：（1）当……2分

    ∴

即为所求切线方程。………………4分

（2）当

令………………6分

∴递减，在（3，+）递增

∴的极大值为…………8分

（3）

①若上单调递增。∴满足要求。…10分

②若

∵恒成立，

恒成立，即a>0……………11分

时，不合题意。综上所述，实数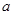的取值范围是

 

已知函数f(x)=

a+sinx

2+cosx

-bx（a、b∈R），
（Ⅰ）若f（x）在R上存在最大值与最小值，且其最大值与最小值的和为2680，试求a和b的值；
（Ⅱ）若f（x）为奇函数：
（1）是否存在实数b，使得f（x）在(0，

2π

3

)为增函数，(

2π

3

，π)为减函数，若存在，求出b的值，若不存在，请说明理由；
（2）如果当x≥0时，都有f（x）≤0恒成立，试求b的取值范围．