
题目列表(包括答案和解析)
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
(本小题满分16分)
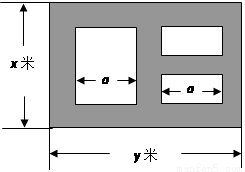
某市近郊有一块大约500m×500m的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米。
(1)分别用x表示y和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值。
(本小题满分12分)
经统计,某大医院一个结算窗口每天排队结算的人数及相应的概率如下:
| 排队人数 | 0—5 | 6—10 | 11—15 | 16—20 | 21—25 | 25人以上 |
| 概 率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1) 每天不超过20人排队结算的概率是多少?
(2) 一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,医院就需要增加结算窗口,请问该医院是否需要增加结算窗口?
(文科做)(本小题满分16分)
已知椭圆 过点
过点 ,离心率为
,离心率为 ,圆
,圆 的圆心为坐标原点,直径为椭圆的短轴,圆
的圆心为坐标原点,直径为椭圆的短轴,圆 的方程为
的方程为 .过圆
.过圆 上任一点
上任一点 作圆
作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)求椭圆的方程;
(2)若直线 与圆
与圆 的另一交点为
的另一交点为 ,当弦
,当弦 最大时,求直线
最大时,求直线 的直线方程;
的直线方程;
(3)求 的最值.
的最值.
(本小题满分12分)2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
|
动作 |
K |
D |
||
|
得分 |
100 |
80 |
40 |
10 |
|
概率 |
|
|
|
|
乙系列:
|
动作 |
K |
D |
||
|
得分 |
90 |
50 |
20 |
0 |
|
概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I) 若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II) (II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com