
题目列表(包括答案和解析)
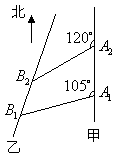
(2007山东理20)如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于![]() 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,此时两船相距
处,此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
(2007
山东,7)命题“对任意的 ,
, ”的否定是
”的否定是
[
]A
.不存在 ,
,
B
.存在 ,
,
C
.存在 ,
,
D
.对任意的 ,
,
(2007
山东,22)设函数 ,其中b≠0.
,其中b≠0.
(1)
当 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;
(2)
求函数f(x)的极值点;(3)
证明对任意的正整数n,不等式 都成立.
都成立.(2007
山东,8)某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;……第六组,成绩大于等于18秒且小于等于19秒.如图所示是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为
[
]|
A .0.9,35 |
B .0.9,45 |
C .0.1,35 |
D .0.1,45 |
(2007
·山东淄博)已知p:对任意a∈[1,2],不等式 恒成立;q:函数
恒成立;q:函数 存在极大值和极小值.求使“p且
存在极大值和极小值.求使“p且 ”为真命题的m的取值范围.
”为真命题的m的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com