
题目列表(包括答案和解析)
甲乙两位同学利用图示实验装置实验。
(1)如图是甲同学利用“探究小车加速度与力的关系”的实验装置来“探究功与速度变化的关系”,他将光电门固定在水平轨道上的B点,用不同重物通过细线拉同一小车,每次小车都从同一位置A由静止释放。
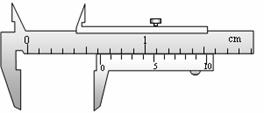
①若用游标卡尺测出光电门遮光条的宽度d如右图所示,则d= cm;实验时将小车从图示位置由静止释放,由数字计时器读出遮光条通过光电门的时间?t=2.0×10-2s,则小车经过光电门时的速度为 m/s;
②实验中可近似认为细线对小车的拉力与重物重力大小相等,则重物的质量m与小车的质量M间应满足的关系为 ;
③测出多组重物的质量m和对应遮光条通过光电门的时间?t,并算出相应小车经过光电门时的速度v,通过描点作出线性图象。处理数据时应作出_________(选填“v—m”或“v2—m”)图象;
④甲同学在③中作出的线性图象不通过坐标原点,可能是由于开始实验测量前,他采取了以下哪些做法________
A.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做匀速运动
B.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做加速运动
C.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动
D.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做加速运动
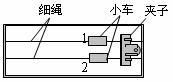
(2)乙同学对实验装置进行修改,用下图实验装置示意图做实验.两个质量相等的小车1、2分别放在水平桌面上,车中可放砝码,车前端各系一条细绳,绳的另一端跨过定滑轮各挂一个小盘,盘里也可放砝码.两个小车通过细线用夹子固定,打开夹子,小盘和砝码牵引小车运动,合上夹子,两小车同时停止.小车1、2所受拉力分别为F1、F2,车与车中所放砝码总质量分别为m1、m2,打开夹子经过相同时间两车位移分别为x1、x2,则( )
A.当m1=m2、F1=2F2时,x1=2x2
B.当m1=m2、F1=2F2时,x2=2x1
C.当m1=2m2、F1=F2时,x1=2x2
D.当m1=2m2、F1=F2时,x2=2x1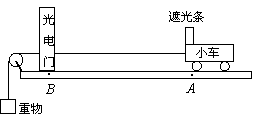
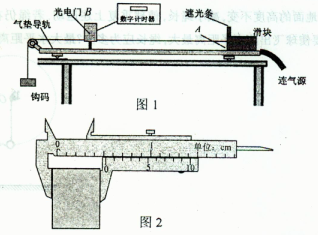

某实验小组利用图1的装置验证钩码和滑块组成的系统机械能守恒,在水平桌面上固定一气垫导轨,导轨上A点处有一带长方形遮光条的滑块,其总质量为M,左端由跨过轻质光滑定滑轮的细绳与一质量为m的钩码相连,且M:m =3:1,遮光条两条长边与导轨垂直,导轨上B点处有一光电门,可以测量遮光条经过光电门时的挡光时间△t,用d表示遮光条的宽度,s表示A、B两点的距离,g表示当地的重力加速度.(计算结果保留两位有效数字)
【小题1】用游标卡尺测量遮光条的宽度d如图2所示,则d= ;
【小题2】实验时,将滑块从位置A由静止释放,由数字计时器读出遮光条通过光电门的时间△t=1.3×10-2s,则滑块经过光电门B时的瞬时速度的值为 ;
【小题3】改变光电门的位置进行多次实验,每次均令滑块自A点开始运动,测量相应的s与△t的值,并计算出经过光电门的瞬时速度v,作出v2 – s图象,若不考虑误差,认为系统的机械能守恒,则v2与s应满足的关系式为:v2= .(用题中所给的符号表示)
【小题4】实验中,利用数据作出的v2 – s图象如图3所示,如果不考虑误差,认为系统的机械能守恒,则可求得当的重力加速度的值g= .
【小题5】如果当地的重力加速度的真实值为10m/s2,则滑块与钩码组成的系统在运动过程中受到阻力的值与钩码重力的值之比为 。
某小组在进行“用单摆测定重力加速度”的实验,已知单摆摆动的摆角小于5°,
(1)单摆的摆长应是球自然下垂时从悬点量至 的距离,此实验在测量周期应从摆球摆到 处开始计时。
(2)某同学先用毫米刻度尺测得悬挂后的摆线长为L,再用游标卡尺测得摆球的直径为d ,如图所示。则该摆球的直径为_____________毫米。
(3)在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t; 该单摆在摆动过程中的周期为 。
(4) 某同学用秒表测得球第40次经过最低点的时间如图所示,则秒表读数为 s;单摆的周期为 s。
(5)用上述物理量的字母符号写出求重力加速度的一般表达式g = .
(6)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中
的 .
| A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了 |
| B.把n次摆动时间误记为(n+1)次摆动的时间 |
| C.以摆线长作为摆长来计算 |
| D.以摆线长与摆球的直径之和作为摆长来计算 |
某小组在进行“用单摆测定重力加速度”的实验,已知单摆摆动的摆角小于5°,
(1)单摆的摆长应是球自然下垂时从悬点量至 的距离,此实验在测量周期应从摆球摆到 处开始计时。
(2)某同学先用毫米刻度尺测得悬挂后的摆线长为L,再用游标卡尺测得摆球的直径为d ,如图所示。则该摆球的直径为_____________毫米。

(3)在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t; 该单摆在摆动过程中的周期为 。
(4) 某同学用秒表测得球第40次经过最低点的时间如图所示,则秒表读数为 s;单摆的周期为 s。

(5)用上述物理量的字母符号写出求重力加速度的一般表达式g = .
(6)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中
的 .
A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动时间误记为(n+1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算
(7)为了提高实验精度,在实验中可改变几次摆长l并测出相应的周期T,从而得出一组对应的l与T的数据,再以l为横坐标、T2为纵坐标将所得数据连成直线,并求得该直线的斜率k。则重力加速度g=________。(用k表示)若根据所得数据连成的直线的延长线没过坐标原点,而是与纵轴的正半轴相交于一点,则由此图象求得的重力加速度的g (填“偏大”,“偏小”,“无影响”)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com